[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
[3]
[4]
Основные определения
Понятие множества является
фундаментальным неопределяемым понятием.
| Определение |
| Под множеством
будем понимать совокупность определенных вполне
различаемых объектов, рассматриваемых как
единое целое. |
Можно говорить о множестве стульев в комнате,
людей, живущих в г. Рязани, студентов в группе, о
множестве натуральных чисел, букв в алфавите,
состояний системы и т. п. При этом о множестве
можно вести речь только тогда, когда элементы
множества различимы между собой. Например,
нельзя говорить о множестве капель в стакане
воды, так как невозможно четко и ясно указать
каждую отдельную каплю.
Отдельные объекты, из которых состоит
множество, называют элементами множества.
Так, число 3—элемент множества натуральных
чисел, а буква б—элемент множества букв
русского алфавита.
Общим обозначением множества служит пара
фигурных скобок { }, внутри которых
перечисляются элементы множества. Для
обозначения конкретных множеств используют
различные прописные буквы A, S, X... или
прописные буквы с индексами А1, А2. Для
обозначения элементов множества в общем виде
используют различные строчные буквы а , s, х
... или строчные буквы с индексами а1, а2 ...
Для указания того, что некоторый элемент а
является элементом множества S, используется символ
 принадлежности
множеству. Запись a
принадлежности
множеству. Запись a S означает, что элемент а принадлежит
множеству S, а запись x
S означает, что элемент а принадлежит
множеству S, а запись x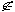 S означает, что элемент х не
принадлежит множеству S.
S означает, что элемент х не
принадлежит множеству S.
Записью х1, х2, ..., xn  S пользуются в
качестве сокращения для записи x1
S пользуются в
качестве сокращения для записи x1 S,
x2
S,
x2 S, . . ., xn
S, . . ., xn S.
S.
Множества бывают конечными и бесконечными.
| Определение |
|
Множество называют конечным, если число его элементов
конечно, т. е. если существует натуральное
числоN, являющееся числом элементов
множества. Множество называют бесконечным,
если оно содержит бесконечное число элементов.
|
Для того, чтобы оперировать с конкретными
множествами, нужно уметь их задавать. Существуют
два способа задания множеств: перечисление и
описание. Задание множества способом
перечисления соответствует перечислению всех
элементов, составляющих множество. Так,
множество отличников группы можно задать,
перечислив студентов, которые учатся на отлично,
например {Иванов, Петров, Сидоров}. Для
сокращения записи X={x1, х2, ..., xn}
иногда пишутX={хi}1n или
вводят множество индексов i={1, 2,...,n}и пишут X={xi},
i  I. Такой
способ удобен при рассмотрении конечных
множеств, содержащих небольшое число элементов,
но иногда он может применяться и для задания
бесконечных множеств, например {2, 4, 6, 8 ... }.
Естественно, что такая запись применима, если
вполне ясно, что понимается под многоточием.
I. Такой
способ удобен при рассмотрении конечных
множеств, содержащих небольшое число элементов,
но иногда он может применяться и для задания
бесконечных множеств, например {2, 4, 6, 8 ... }.
Естественно, что такая запись применима, если
вполне ясно, что понимается под многоточием.
Описательный способ задания множества состоит в
том, что указывается характерное свойство,
которым обладают все элементы множества. Так,
если М—множество студентов группы, то
множество А отличников этой группы запишется
в виде
A={x M | x
— отличник группы},
M | x
— отличник группы},
что читается следующим образом: множество А
состоит из элементов х множества М,
обладающих тем свойством, что х является
отличником группы. В тех случаях, когда не
вызывает сомнений, из какого множества берутся
элементы х, указание о принадлежности
множеству М можно не делать. При этом
множество А запишется в видеА={х | х -
отличник группы}.
Приведем несколько примеров задания множеств
методом описания:
{х | х — четное} — множество четных чисел;
{х | х2 — 1= 0} - множество{+1, —1}.
Пусть С — множество целых чисел. Тогда {х
 С | 0 < х
С | 0 < х 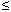 7} есть
множество {1, 2, 3, 4, 5, 6, 7}. Важным понятием
теории множеств является понятие пустого
множества.
7} есть
множество {1, 2, 3, 4, 5, 6, 7}. Важным понятием
теории множеств является понятие пустого
множества.
| Определение |
|
Пустым множеством, называют множество, не содержащее ни одного элемента.
|
Пустое множество обозначается 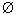 , например:
, например:
{х С | х2 -
х+1=0} =
С | х2 -
х+1=0} = 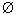
Понятие пустого множества играет очень важную
роль при задании множеств с помощью описания.
Так, без понятия пустого множества мы не могли бы
говорить о множестве отличников группы или о
множестве вещественных корней квадратного
уравнения, не убедившись предварительно,есть ли
вообще в данной группе отличники или имеет ли
данное уравнение вещественные корни. Введение
пустого множества позволяет совершенно спокойно
оперировать с множеством отличников группы, не
заботясь о том, есть или нет в рассматриваемой
группе отличники.
Пустое множество будем условно относить к
конечным множествам. Рассмотрим теперь вопрос о
равенстве множеств.
| Определение |
|
Два множества называются равными,
если они состоят из одних и тех же элементов, т. е.
представляют собой одно и то же множество.
|
Множества Х и Y не равны (X 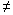 Y),если либо в
множестве Х есть элементы, не принадлежащиеY,
либо в множество Y есть элементы, не
принадлежащие X. Y),если либо в
множестве Х есть элементы, не принадлежащиеY,
либо в множество Y есть элементы, не
принадлежащие X.
|
Символ равенства множеств обладает свойствами:
- Х=Х —рефлексивность;
- если X = Y, то Y = X — симметричность;
- если X = Y и Y = Z, то X = Z —транзитивность.
Из определения равенства множеств вытекает,
что порядок элементов в множестве
несуществен.
Так, например, множества {3, 4, 5, 6}
и {4, 5, 6, 3} представляют собой одно и то же
множество. Из определения множества следует, что
в нем не должно быть неразличимых элементов.
Поэтому в множестве не может быть одинаковых
элементов. Запись{2, 2, 3, 5} следует
рассматривать как некорректную и заменить ее на {2,
3, 5}. Так, множество простых делителей числа 60
равно {2, 3, 5}.
[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
[3]
[4]
 принадлежности
множеству. Запись a
принадлежности
множеству. Запись a S означает, что элемент а принадлежит
множеству S, а запись x
S означает, что элемент а принадлежит
множеству S, а запись x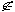 S означает, что элемент х не
принадлежит множеству S.
S означает, что элемент х не
принадлежит множеству S.  S пользуются в
качестве сокращения для записи x1
S пользуются в
качестве сокращения для записи x1 S,
x2
S,
x2 S, . . ., xn
S, . . ., xn S.
S.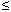 7} есть
множество {1, 2, 3, 4, 5, 6, 7}. Важным понятием
теории множеств является понятие пустого
множества.
7} есть
множество {1, 2, 3, 4, 5, 6, 7}. Важным понятием
теории множеств является понятие пустого
множества.
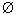 , например:
, например: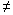 Y),если либо в
множестве Х есть элементы, не принадлежащиеY,
либо в множество Y есть элементы, не
принадлежащие X.
Y),если либо в
множестве Х есть элементы, не принадлежащиеY,
либо в множество Y есть элементы, не
принадлежащие X.