[Список тем]

Алгебра Жегалкина и линейные функции

Алгебра Жегалкина - это алгебра над множеством двух бинарных булевых функций (И,) и нульарной функции 1.
Легко проверить следующие соотношения этой алгебре:
pq = qp;
p(qpqr) = pq pr;
pp = 0;
p0 = p.

Справедливы в этой алгебре, конечно, и все соотношения, включающие логические функции. Если в произвольной формуле, включающей только функции базиса Жегалкина, раскрыть скобки, то получим бесскобочную формулу, имеющую вид суммы (по модулю два) произведений, то есть некоторый полином. Он называется полиномом Жегалкина.

Пример:

Преобразуем аналитически функцию f (p, q, г) = р v q rq(p v r) в полиномом Жегалкина.
Поскольку q = 1 p, a
p v q = ( p q) = 1 (1p) (1q) = pq pq, то после подстановки и раскрытия скобок имеем:

f(p, q, r) = p v q rq (p v r) = ((1 p) q (1p)q) (rq(pr pr)) =

= (1pqqpq)(pqrqrpqr) = 1ppqqr.

Теорема
Любая булева функция может быть представлена в виде полинома Жегалкина, причем единственным образом.

Доказательство.

Существование полинома для любой функции гарантируется тем, что функции {И, , 1} образуют базис. Далее, легко видеть, что число возможных членов в полиноме с m переменными равно 2^m. Поэтому число различных полиномов Жегалкина от m переменных равно 2 в степени 2^m, то есть числу возможных двоичных функций от m переменных. Поскольку одна и та же формула не может представлять различные функции, то тем самым между множествами двоичных функций и полиномов Жегалкина от m переменных установлено взаимнооднозначное соотношение.

Пример

Построим для функции f (p, q, r) = p v q rq (p v r) полиномом Жегалкина непосредственно из таблицы истинности.

p	q	r	f
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	0

Будем искать коэффициенты полинома

f (p, q, r) = а₀ a_pp a_qq a_rr a_prpr a_qrqra_pqrpqr.

Всего коэффициентов 8, каждый коэффициент может быть 0 или 1, число возможных вариантов равно 2⁸ = 256 - как раз столько, сколько всех возможных булевых функций от-трех переменных. Для нахождения коэффициентов заданной функции используем таблицу ее значений.

Искомые коэффициенты последовательно найдем из следующей системы уравнений:
f (0,0,0) = 1 = a₀; отсюда a₀=1;
f (1,0,0) = 0 = a₀ a_p = 1a_p; отсюда a_p=1;
f (0,1,0) = 1 = a₀ a_q = 1a_q; отсюда a_q=0;
f (0,0,1) = 1 = a₀ a_r = 1a_r; отсюда a_r=0;
f(1,1,0) = 1 = a₀ a_p a_q a_pq = 11 0 a_pq; отсюда a_pq = 1;
f(1,0,1) = 0 = a₀ a_p a_r a_pr = 11 0 a_pr; отсюда a_pr = 1;
f(0,1,1) = 0 = a₀ a_q a_r a_qr = 10 0 a_qr; отсюда a_qr = 1;
f(1,1,1) = 0 = a₀ a_pa_q a_r a_pq a_pr a_qra_pqr = 1 1 0 0 1 0 1 a_pqr; отсюда a_pqr=0;

Найденное представление совпадает с представлением, полученным для этой функции ранее аналитически: f(p,q,r) = 1p pq qr.
Булева функция, полиномом Жегалкина которой имеет вид a₀ 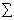a_xi x _i, называется линейной.

[Список тем]