[Список тем]

Минимизация логических выражений методом карт Вейча

Количество клеток в карте Вейча соответствует количеству строк в таблице истинности логической функции.
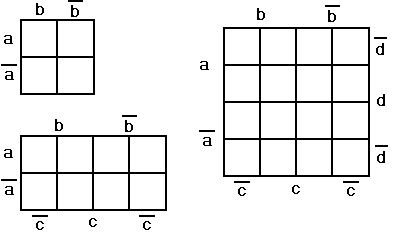
В зависимости от количества переменных карта Вейча может иметь вид:

Главное свойство карты Вейча состоит в том, что при переходе в любую соседнюю клетку по вертикали и горизонтали (включая переходы из крайней клетки в клетку лежащую на противоположном краю), в составе переменных, определяющих расположение клеток, меняет свой знак только одна переменная. Т.е. одинаковые логические значения в соседних клетках позволяют проводить операции склеивания и поглощения.

Соответствие клеток логическим значениям переменных для функции четырех переменных показано на рисунках.

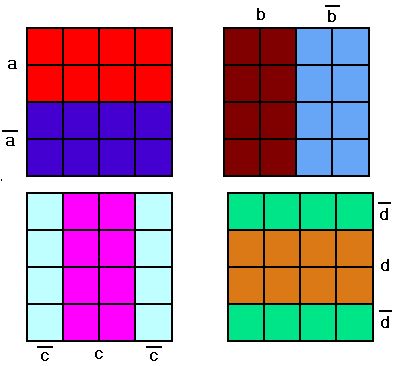
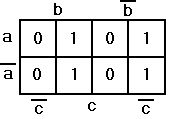
Заполнение карты по таблице истинности осуществляется по значениям переменных в строках таблицы. Первой строке соостветствуют значения a=0; b=0; c=0. На карте Вейча этому сочетанию значений соответствует правая нижняя клетка. Второй строке таблицы истинности (0 0 1) соответствует соседняя клетка. И т.д в соответствии с номерами клеток на рисунке.

Т. о. в правую нижнюю клетку мы вставим логическое значение функции из первой строки f(a,b,c)=1, в соседнюю клетку f(a,b,c)=0 из второй строки и т. д.

a b c f(a,b,c) 0 0 0 1 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1

Для быстрого заполнения карты с четырьмя переменными надо запомнить порядок заполнения клеток.

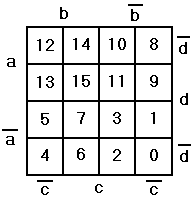
Номер заполняемой клетки соответствует двоичному числу, которое образуют аргументы функции данной строки.

a b c d f(a,b,c,d) 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 1 1 1 0 1 0 0 1 0 1 0 1 0 0 1 1 0 0 0 1 1 1 1 1 0 0 0 0 1 0 0 1 0 1 0 1 0 1 1 0 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 0 1 1 1 1 1 1

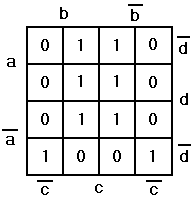Получение МДНФ
МДНФ логической функции получают по единичным значениям. Все клетки, содержащие 1, объединяются в замкнутые прямоугольные области с числом клеток 2k, т.е. допустимое число клеток 1, 2, 4, 8,… Области могут пересекаться. Одни и те же клетки могут входить в разные области, но каждая клетка с 1 должна входить хотя бы в одну из областей. При объединении карту мысленно сворачивают в трубку по вертикали и горизонтали т.е. соседними являются клетки на противоположных сторонах карты и все четыре угловые клетки одновременно.
Каждая из областей представляется в МДНФ элементарной конъюнкцией, составленной только из тех (n-k) переменных, которые для клеток данной области имеют одинаковое значение (без инверсии либо с инверсией).
Следует стремиться, чтобы число областей было минимальным (при этом в МДНФ будет минимальное число слагаемых), а в каждой области содержалось как можно больше клеток (минимальным будет количество переменных в каждой элементарной конъюнкции).

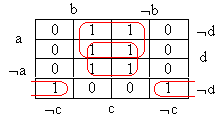
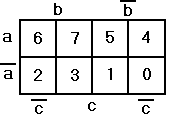
МДНФ функции:
f(a,b,c,d) = ac cd 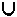¬ a ¬ c ¬ d
Каждая область из 4 единиц отображается двумя переменными, из 2 единиц - тремя, а если клетку вообще не удастся объединить ни с какой другой, то понадобятся все 4 аргумента функции.

Получение МКНФ
Для получения МКНФ логической функции в карте Вейча замкнутыми прямоугольными областями охватывают соседние клетки содержащие 0. При записи членов логического выражения берутся инверсии аргументов функции на пересечении которых находятся области.

МКНФ: f(a,b,c,d) = b & (c d)

Внимание!
Нельзя объединять в замкнутые прямоугольные области две клетки с одинаковыми логическими значениями, если есть возможность объединить четыре. Во всех случаях, когда объединяемые Вами клетки имеют еще 2, 4, 8 соседних клеток, объединять надо максимально возможное число клеток, иначе полученная форма не будет минимальной.

Упражнения.

a	b	c	d	f1	f2	f3	f4
0	0	0	0	1	1	0	1
0	0	0	1	1	0	0	0
0	0	1	0	0	0	1	1
0	0	1	1	1	0	0	0
0	1	0	0	1	1	0	0
0	1	0	1	1	0	0	0
0	1	1	0	0	0	1	1
0	1	1	1	1	1	0	0
1	0	0	0	0	1	0	0
1	0	0	1	1	1	1	1
1	0	1	0	0	1	0	1
1	0	1	1	0	0	1	0
1	1	0	0	0	1	0	0
1	1	0	1	1	1	1	1
1	1	1	0	0	0	0	1
1	1	1	1	0	0	1	0

[Список тем]