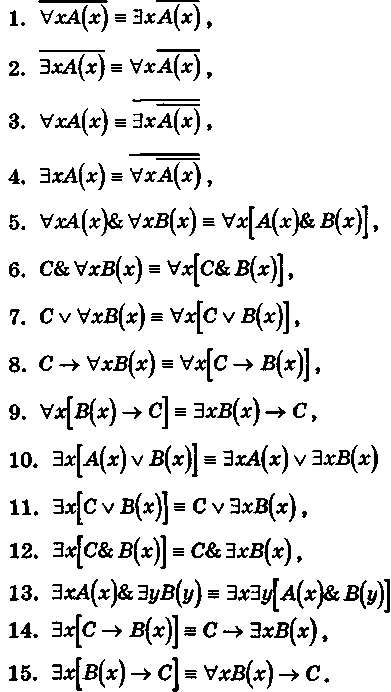
[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]
| Определение |
|---|
| Две формулы логики предикатов А и В называются равносильными на области М, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области М. |
| Определение |
|---|
| Две формулы логики предикатов А и В называются равносильными, если они равносильны на всякой области. |
Здесь, как в алгебре высказываний, для равносильных формул принято обозначение
A ≡ В.
Ясно, что все равносильности алгебры высказываний будут верны, если в них
вместо переменных высказываний подставить формулы логики предикатов. Но, кроме
того, имеют место равносильности самой логики предикатов. Рассмотрим основные
из этих равносильностей. Пусть A(х) и В(х) - переменные
предикаты, а С - переменное высказывание. Тогда
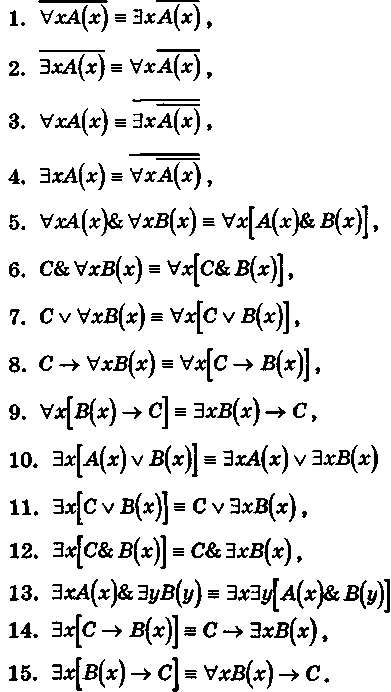
Равносильность 1 означает тот простой факт, что, если не для всех х истинно A(х),
то существует х, при котором будет истиной ¬A(х).
Равносильность 2 означает тот простой факт, что, если не существует х, при котором
истинно A(х) , то для всех х будет истиной ¬A(х).
Равносильности 3 и 4 получаются из равносильностей 1. и 2. соответственно, если от обеих
их частей взять отрицания и воспользоваться законом двойного отрицания.
Докажем равносильность 5. Если предикаты A(х) и В(х) одновременно тождественно
истинные, то будет тождественно истинным и предикат А(х)&В(х), а поэтому будут
истинными высказывания:
 хА(х),
хА(х),  xB(x),
xB(x),  x[A(x)&B(x)]
x[A(x)&B(x)]
То есть в этом случае обе части равносильности 5 принимают значение “истина”.
Пусть теперь хотя бы один из предикатов, например, A(х), будет не тождественно истинным.
Тогда не тождественно истинным будет и предикат A(х) & B(x) , a поэтому ложными будут высказывания
 xA(x),
xA(x),  xA(x)&
xA(x)& xB(x),
xB(x),
 x[A(x)&B(x)],
x[A(x)&B(x)],
то есть и в этом случае обе части равносильности 5 принимают одинаковые (ложные) значения.
Этим исчерпывается доказательство равносильности 5.
Докажем равносильность 8. Пусть переменное высказывание С принимает значение “ложь”.
Тогда тождественно истинным будет предикат С 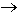 B(x) и, очевидно, истинными будут
высказывания С
B(x) и, очевидно, истинными будут
высказывания С 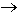
 xB(x) и
xB(x) и  x[
С
x[
С 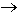 B(x)],
B(x)],
то есть в этом случае обе части равносильности 8 принимают одинаковые (истинные) значения.
Пусть теперь переменное высказывание С принимает значение “истина”. Если при этом
переменный предикат является тождественно истинным, то будет тождественно истинным и предикат
С 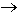 В(х), и, значит, истинными будут высказывания
В(х), и, значит, истинными будут высказывания  xВ(x),
С
xВ(x),
С 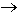
 xB(x) ,
xB(x) ,  x[C
x[C 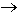 B(x)] ,
то есть и в этом случае обе части равносильности 8 принимают одинаковые (истинные) значения.
B(x)] ,
то есть и в этом случае обе части равносильности 8 принимают одинаковые (истинные) значения.
Если же предикат B(х) не является тождественно истинным, то не будет тождественно
истинным и предикат С 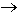 B(x) , а поэтому ложными будут высказывания
B(x) , а поэтому ложными будут высказывания
 хВ(х), C
хВ(х), C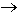
 xB(x),
xB(x),
 x[C
x[C 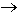 B(x)].
B(x)].
Следовательно, и здесь обе части равносильности 8 принимают одинаковые (ложные) значения.
Этим исчерпывается доказательство равносильности 8.
Аналогично доказывают остальные из перечисленных равносильностей.
В заключение отметим, что формула  x[A(x)
x[A(x)
 В(x)] не равносильна формуле
В(x)] не равносильна формуле
 xA(x)
xA(x) 
 xB(x), а формула
xB(x), а формула  x[A(x)&B(x)] не
равносильна формуле
x[A(x)&B(x)] не
равносильна формуле  хА(х)&
хА(х)&  хВ(х).
Однако, справедливы равносильности
хВ(х).
Однако, справедливы равносильности
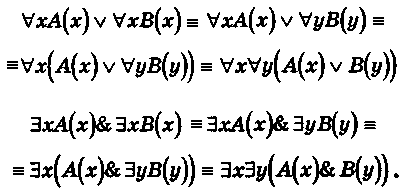
[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]