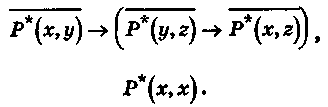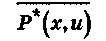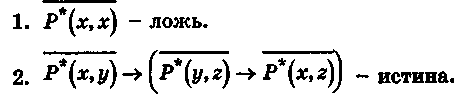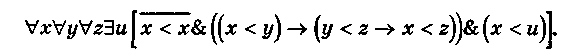[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]

Общезначимость и выполнимость формул

Определение 1
Формула А логики предикатов называется выполнимой в области М, если существуют значения переменных, входящих в эту формулу и отнесенных к области М, при которых формула А принимает истинные значения.

Определение 2
Формула А называется выполнимой, если существует область, на которой эта формула выполнима.

Из определения 2 следует, что, если формула выполнима, то это еще не означает, что она выполнима в любой области.

Определение 3
Формула А называется тождественно истинной в области М, если она принимает истинные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области.

Определение 4
Формула А называется общезначимой, если она тождественно истинная на всякой области.

Определение 5
Формула А называется тождественно ложной в области М, если она принимает ложные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области.

Из приведенных определений следует:
Если формула А общезначима, то она и выполнима на всякой области. Если формула А тождественно истинная в области М, то она и выполнима в этой области. Если формула А тождественно ложная в области М, то она не выполнима в этой области. Если формула А не выполнима, то она тождественно ложна на всякой области.

Всвязи с данными определениями естественно выделить два класса формул логики предикатов: выполнимых и не выполнимых формул.
Отметим, что общезначимую формулу называют логическим законом.

Приведем соответствующие примеры:

• Пример 1. Формула хуР(х, у) выполнима. Действительно, если P(x, у) - предикат “ х < у ”, определенный в области M = Е х Е, где Е ={0,1,2,...,n,...} , то формула хуР(х, у) тождественно истинная в области М, и, следовательно, выполнима в этой области. Однако, если предикат “ х < у ” рассматривается в конечной области M = Е₁ х Е₁ , где Е₁ ={0,l,2,...,k} , то формула х уР(х, у) будет тождественно ложной в области M₁, и, следовательно, не выполнима в области М₁. При этом ясно, что формула хуР(х, у) не общезначима.
  
• Пример2. Формула ху[Р(х)& P(у)] выполнима.
  Действительно, если P(x) - предикат “Число x - четно”, определенный в области М = Е х Е, где Е = {0,1,2,...,n,...}, то эта формула тождественно истинная в области М, и, следовательно, выполнима в области М. Однако, если предикат “Число х - четно” рассматривать в области M₁=E₁x E₁, где E_l - множество четных чисел, то формула ху[Р(х) & P(у)] будет тождественно ложной в области М₁, и, следовательно, не выполнимой.
  
• Пример 3. Формула х [Р(х) v P(x)] тождественно истинная в любой области М. Значит, она является общезначимой, то есть является логическим законом (закон исключенного третьего).
  
• Пример 4. Формула х [Р(х) & P(x)] тождественно ложная в любой области М, и поэтому она не выполнима.

Легко установить связь между общезначимостью и выполнимостью формул логики предикатов.

Теорема 1.
Для того, чтобы формула А была общезначима, необходимо и достаточно, чтобы ее отрицание было не выполнимо.

Доказательство. Необходимость. Пусть формула А общезначима. Тогда, очевидно, А — тождественно ложная формула в любой области, и поэтому формула А не выполнима.
Достаточность. Пусть формула А не выполнима в любой области. Тогда по определению невыполнимой формулы А — тождественно ложная в любой области. Значит, формула А - тождественно истинная формула в любой области, и, следовательно, она общезначима.

Теорема 2.
Для того, чтобы формула А была выполнимой, необходимо и достаточно, чтобы формула А была не общезначима.

Доказательство. Необходимость. Пусть формула А выполнима. Это означает, что существует область М и набор значений переменных, входящих в формулу А, при которых формула А принимает истинное значение. Очевидно, что на этом наборе значений переменных формула А принимает ложное значение, и, следовательно, формула А необщезначима.
Достаточность. Пусть формула А не общезначима. Тогда существует область М и набор значений переменных, входящих в формулу, при которых формула А принимает ложное значение. На этом наборе значений переменных формула А принимает значение “истина”, и поэтому формула А выполнима.

Пример формулы, выполнимой в бесконечной области и невыполнимой ни в какой конечной области
Покажем, что формула

выполнима в бесконечной области и невыполнима ни в какой конечной области.
Допустим, что формула (1) выполнима в некоторой области М. В таком случае должен существовать фиксированный предикат Р*(х,у), для которого формула (1) принимает значение 1. Тогда для всех элементов х, у, z и хотя бы для одного элемента u из области М формула

принимает значение 1. Но в этом случае принимают значение 1 и формулы

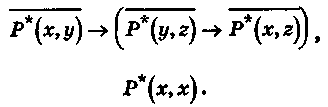
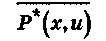
тоже принимает значение 1.
Нетрудно убедиться, что в таком случае предикат (Р*(х,у))представляет собой предикат, устанавливающий отношение порядка между элементами области М. Действительно, из истинности формул (2) и (3) следует, что предикат (Р*(х,у)) удовлетворяет аксиомам порядка:

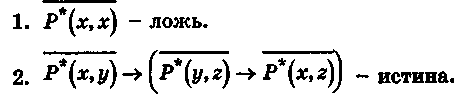
В связи с этим условимся (Р*(х,у)) выражать словами "x предшествует у". Как видно из истинности формулы (4), для каждого х должно существовать такое u, что истинно (Р*(х,u)), то есть “x предшествует u”. Возьмем произвольный элемент области х₁; среди элементов области должен найтись такой элемент х₂, что "х₂ предшествует х₂" . Точно также должен найтись такой элемент x₃ что “х₂ предшествует x₃” и т. д. Получаем последовательность элементов
x₁, x₂,..., x_n,... (5)
В силу аксиом 1 и 2 каждый элемент этой последовательности отличен от каждого элемента с меньшим индексом, так как будет иметь место "x₁ предшествует x_n". Но это означает, что любые два элемента последовательности (5) различны и область М бесконечна.
Покажем, что существует область, на которой формула (1) выполнима. Пусть М = {0,1,2,...,n,...} , а Р(х,у) означает “х>=у”. Тогда (Р(х,у)) означает “х<у”. При такой замене предиката Р(х,у) формула (1) принимает вид

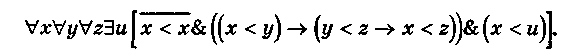
Очевидно, что на множестве М ={0,1,2,...,n,...} эта формула истинна.
Из доказанного ясно, что, если область, на которой рассматривается формула (1), конечна, то формула (1) тождественно ложна на М, и, значит, не выполнима.

[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]