[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
Бинарные отношения на множестве свойства бинарных отношений
| Определение 3 |
|---|
|
Бинарным отношением на множестве Х называется бинарное
(двухместное) отношение на Х х X.
|
Пример 1. Пусть Х = R.
Рассмотрим бинарное отношение а, заданное
правилом:
x α y x2=y2.
x2=y2.
Пример 2. Пусть Х = R. Рассмотрим бинарное
отношение  , заданное правилом:
, заданное правилом:
x  y
y x2 < y2.
x2 < y2.
Пример 3. Пусть Х = С (С — множество
комплексных чисел). Рассмотрим бинарное
отношение 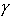 , заданное правилом:
, заданное правилом:
z1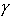 z2
z2  | z1
| = | z2 |.
| z1
| = | z2 |.
Пример 4. Рассмотрим на С бинарное отношение 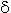 ,
заданное правилом:
,
заданное правилом:
z1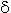 z
2
z
2  ( Re z1 ≤
Re z2 ) & ( Imz1 = Imz2 ).
( Re z1 ≤
Re z2 ) & ( Imz1 = Imz2 ).
Выделяют следующие основные свойства бинарных
отношений: рефлексивность, транзитивность, симметричность, антисимметричность,
а затем с помощью присутствия определенной комбинации этих свойств выделяют
два важнейших типа бинарных отношений: отношения порядка и
отношения эквивалентности.
| Определение 4 |
|---|
Бинарное отношение α на
Х называется рефлексивным, если
 x(xαx) ≡ 1 x(xαx) ≡ 1
Т. е. бинарное отношение а, порожденное
множеством Sa, называется рефлексивным,
если множество Sa, порождающее а,
содержит целиком диагональ декартова квадрата Х
х Х —
diag(X x X) =
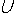 {x;x}; {x;x};
x 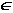 X X
|
| Определение 5 |
|---|
Бинарное отношение α на Х
называется транзитивным, если
 x
x y y z((xα y)&(yα z)→(xαz))
≡1
z((xα y)&(yα z)→(xαz))
≡1
( x x y y
 z((x α y)&(y α z) z((x α y)&(y α z)
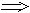 (x α z))). (x α z))).
|
| Определение 6 |
|---|
Бинарное отношение α на Х
называется симметричным, если
 x x y((xαy)→
(yαx)) ≡1 y((xαy)→
(yαx)) ≡1
( x x y((x
αy) y((x
αy)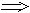 (y α x))). (y α x))).
Т. е. бинарное отношение а на Х
симметрично, если множество Sa, его
порождающее, расположено симметрично относительно diag(X х X).
|
| Определение 7 |
|---|
Бинарное отношение α на Х
называется антисимметричным, если
 x x  y
((xαy) → (x = y))&(y α x) ≡1 y
((xαy) → (x = y))&(y α x) ≡1
( x x y((x α
y)&(y α x) y((x α
y)&(y α x)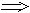 (x=y))). (x=y))).
Т. е. бинарное отношение a на Х
антисимметрично, если множество Sa, его
порождающее, не содержит ни одной пары различных
точек, симметричных относительно diag(X х X) ( рис. 1).
|
Бинарное отношение α на Х
называется несимметричным, если
 x x  y
((xαy) → ¬(y α x) y
((xαy) → ¬(y α x)
Т. е. бинарное отношение a на Х
несимметрично, если множество Sa, его
порождающее, не содержит ни одной пары точек, симметричных относительно
diag(X х X), и не содержит точек самой диагонали.
|
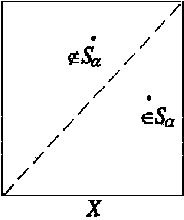
Рис.1
Пример 5. Рассмотрим таблицу:
| |
рефлек-
сивность |
симмет-
ричность |
транзи-
тивность |
антисим-
метричность |
| α |
+ |
+ |
+ |
- |
 |
- |
- |
+ |
+ |
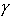 |
+ |
+ |
+ |
- |
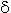 |
+ |
- |
+ |
+ |
| = |
+ |
+ |
+ |
+ |
| ≤ |
+ |
- |
+ |
+ |
x ≤|y|, x, y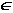 R R |
+ |
- |
- |
- |
Здесь “+” означает, что соответствующее
свойство присутствует, а “—” отсутствует, α,
 ,
, 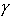 ,
, 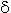 —отношения из примеров 7 - 10.
—отношения из примеров 7 - 10.
Отношение порядка
| Определение 8 |
|---|
|
Бинарное отношение α на Х
называется отношением нестрогого порядка на X, если оно
рефлексивно, транзитивно и антисимметрично.
|
Классическим примером отношения нестрогого порядка
является отношение <= на R.
Ясно что отношение 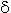 (см. пример 2) является
отношением порядка на С.
(см. пример 2) является
отношением порядка на С.
| Определение 8a |
|---|
|
Бинарное отношение α на Х
называется отношением строгого порядка на X, если оно
антирефлексивно, транзитивно и несимметрично.
|
Примером отношения строгого порядка
является отношение < на R.
Отношение порядка α на Х называется
отношением линейного порядка на Х (линейным
порядком на X), если
 x
x  y((x αy)
y((x αy)
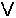 (y α x))
≡1
(y α x))
≡1
В противном случае порядок называется частичным.
То есть отношение порядка на Х является
линейным порядком, если любые два элемента
множества Х сравнимы этим отношением.
Ясно, что отношение <= на R является
отношением линейного порядка, а отношение 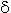 на С —
частичного порядка, так как 1 + i ¬
на С —
частичного порядка, так как 1 + i ¬ 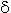 2 - 2i и 2
-2i ¬
2 - 2i и 2
-2i ¬ 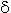 1+i.
1+i.
Пример 6. Рассмотрим произвольное множество
А и на множестве 2A - бинарное отношение 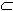 .
Ясно, что
.
Ясно, что 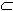 является отношением порядка,
причем если |А| <= 1 — порядок линейный, а если
|A| >= 2 — частичный.
является отношением порядка,
причем если |А| <= 1 — порядок линейный, а если
|A| >= 2 — частичный.
Пара (Х,а), где а — бинарное
отношение на X, называется упорядоченным
множеством, если а — отношение порядка на
X; линейно - упорядоченным множеством, если а
— линейный порядок; частично - упорядоченным
множеством, если а — частичный порядок.
Ясно, что (R, <= ) — линейно - упорядоченное
множество, а (С, 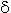 ) (см. пример 2) — частично -
упорядоченное множество.
) (см. пример 2) — частично -
упорядоченное множество.
Доминирование
Пусть (X, а) — упорядоченное множество,
определим на Х еще одно бинарное отношение da
— доминирование.
| Определение 9 |
|---|
Говорят, что у (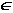 X)
доминирует над х ( X)
доминирует над х (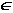 X) по отношению порядка
α (пишут x da
у), если X) по отношению порядка
α (пишут x da
у), если
1) x ≠ y;
2) xα y;
3) z(xαz)&(z αy)→(x=z) z(xαz)&(z αy)→(x=z)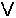 (z=y)
≡ 1 (z=y)
≡ 1
Отношение доминирования антирефлексивно
антисимметрично
не транзитивно
|
Пример 7. Рассмотрим (N, <=). Ясно, что 4
доминирует над 3, 5 над 4.
Пример 8. Пусть С = {1; 2; 3}. На множестве 2c =
{ Ø , {1}, {2}, {3},{1;2}, {1;3}, {2;3},С} рассмотрим отношения
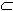 , d
, d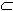 - Элементы множества 2c
изобразим точками, а пару точек x, у соединим
стрелкой от х к у, если xdcy. Тогда
мы получим (рис. 2):
- Элементы множества 2c
изобразим точками, а пару точек x, у соединим
стрелкой от х к у, если xdcy. Тогда
мы получим (рис. 2):
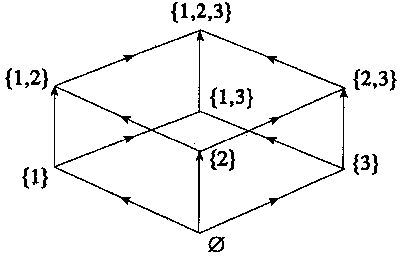
Рис.2
Этот рисунок ( граф) называется диаграммой
Хассе, или диаграммой доминирования.
граф) называется диаграммой
Хассе, или диаграммой доминирования.
Отношение эквивалентности
| Определение 10 |
|---|
|
Бинарное отношение α на множестве Х называется отношением
эквивалентности, если оно рефлексивно, симметрично и транзитивно
|
Пример 9. Отношение "=" на любом
множестве Х является отношением
эквивалентности.
Пример 10. Отношения α
и  примеров 7 и 9
являются отношениями эквивалентности.
примеров 7 и 9
являются отношениями эквивалентности.
Отношение толерантности
| Определение 11 |
|---|
|
Бинарное отношение α на множестве Х называется отношением
толерантности, если оно рефлексивно и симметрично
|
Пример 11. Отношение "быть другом" является отношением толерантности.
[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
 x2=y2.
x2=y2. , заданное правилом:
, заданное правилом:  y
y x2 < y2.
x2 < y2. , заданное правилом:
, заданное правилом: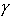 z2
z2  | z1
| = | z2 |.
| z1
| = | z2 |.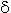 ,
заданное правилом:
,
заданное правилом: 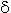 z
2
z
2  ( Re z1 ≤
Re z2 ) & ( Imz1 = Imz2 ).
( Re z1 ≤
Re z2 ) & ( Imz1 = Imz2 ). x(xαx) ≡ 1
x(xαx) ≡ 1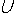 {x;x};
{x;x};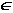 X
X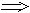 (x α z))).
(x α z))).
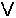 (y α x))
≡1
(y α x))
≡1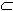 .
Ясно, что
.
Ясно, что 
 граф) называется диаграммой
Хассе, или диаграммой доминирования.
граф) называется диаграммой
Хассе, или диаграммой доминирования.