[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]

Кратчайшие пути

Задача нахождения кратчайшего пути в графе имеет столько практических применений и интерпретаций, что привести примеры Вы можете самостоятельно.
Здесь рассматриваются два классических алгоритма, которые желательно знать каждому программисту.

1. Длина дуг

Алгоритм Уоршалла позволяет ответить на вопрос, существует ли цепь <u, v>. Часто нужно не только определить, существует ли цепь, но и найти эту цепь. Если задан орграф G(V, E), в котором дуги помечены числами (эти числа обычно называют весами, или длинами, дуг), то этот орграф можно представить в виде матрицы весов (длин) С:

Длиной пути называется сумма длин дуг, входящих в этот путь. Наиболее часто на практике встречается задача отыскания кратчайшего пути.

2. Алгоритм Флойда

Алгоритм Флойда находит кратчайшие пути между всеми парами вершин в (ор)графе. В этом алгоритме для хранения информации о путях используется матрица H[1..р,1..р], где

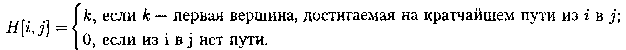
ОТСТУПЛЕНИЕ

Матрица Н размера O(р2) хранит информацию обо всех (кратчайших) путях в графе. Заметим, что всего в графе O(р2) путей, состоящих из O(р) вершин. Таким образом, непосредственное представление всех путей потребовало бы памяти объема O(р3). Экономия памяти достигается за счет интерпретации представления, то есть динамического вычисления некоторой части информации вместо ее хранения в памяти. В данном случае любой конкретный путь <u, v> легко извлекается из матрицы с помощью следующего алгоритма.
w: = u; yield w{ первая вершина }
while w v do
w: = H[w, v]; yield w{ следующая вершина }
end while

Алгоритм 3. алгоритм Флойда

Вход: матрица С[1..р, 1..р] длин дуг.
Выход: матрица T[1..р,1..р] длин путей и матрица H[1..р,1..р] самих путей.
for i from 1 to p do
for j from 1 to p do
T[i, j] := C[i, j] { инициализация }
if C[i, j] = then
H[i, j]: = 0 { нет дуги из i в j }
else
H[i, j]:= j { есть дуга из i в j }
end if
end for
end for
for i from 1 to p do
for j from 1 to p do
for k from 1 to p do
if i j & T[j, i] & i k & T[i, k] &(T[j, k] = T[j, k] > T[j, i]+T[i, k])
then
H[j, k]: = H[j, i] { запомнить новый путь }
T[j, k]: = T[j, i] + T[i, k] { и его длину }
end if
end for
end for
for j from 1 to p do
if T[j, j] < 0 then
stop { нет решения: вершина j входит в цикл отрицательной длины }
end if
end for
end for

ЗАМЕЧАНИЕ

Если в G есть цикл с отрицательным весом, то решения поставленной задачи не существует, так как можно "накручивать" на этом цикле сколь угодно короткий путь.

обоснование
Алгоритм Флойда имеет много общего с алгоритмом Уоршалла (алгоритм 1.8). Покажем по индукции, что после выполнения i-го шага основного цикла по i элементы матриц T[j, k] и H[j, k] содержат, соответственно, длину кратчайшего пути и первую вершину на кратчайшем пути из вершины j в вершину k, проходящем через промежуточные вершины из диапазона 1..i. База: i = 0, то есть до начала цикла элементы матриц Т и Н содержат информацию о кратчайших путях (если таковые есть), не проходящих ни через какие промежуточные вершины. Пусть теперь перед началом выполнения тела цикла на i-м шаге T[j, k] содержит длину кратчайшего пути от j к k , a H[j, k] содержит первую вершину на кратчайшем пути из вершины j в вершину k (если таковой есть). В таком случае, если в результате добавления вершины i к диапазону промежуточных вершин находится более короткий путь (в частности, если это вообще первый найденный путь), то он записывается. Таким образом, после окончания цикла, когда i = р, матрицы содержат кратчайшие пути, проходящие через промежуточные вершины 1..р, то есть искомые кратчайшие пути. Алгоритм не всегда выдает решение, поскольку оно не всегда существует. Дополнительный цикл по j служит для прекращения работы в случае обнаружения в графе цикла с отрицательным весом.

3. Алгоритм Дейкстры

Алгоритм Дейкстры находит кратчайший путь между двумя данными вершинами в (ор)графе, если длины дуг неотрицательны.

алгоритм Дейкстры

Вход: орграф G(V,E), заданный матрицей длин дуг С : array [1..p, 1..p] of real; s и t - вершины графа.
Выход: векторы T : array [1..p] of real; и Н : array [1..p] of 0..p. Если вершина v лежит на кратчайшем пути от s к t, то T[v] - длина кратчайшего пути от s к v; Н[v] - вершина, непосредственно предшествующая v на кратчайшем пути.
for v from 1 to p do
T[v]: = { кратчайший путь неизвестен }
X[v]: =0 { все вершины не отмечены }
end for
H[s]:= 0 { s ничего не предшествует }
T[s]: =0 { кратчайший путь имеет длину 0 ... }
X[s]:=l { ... и он известен }
v: = s { текущая вершина }
М: { обновление пометок }
for u Г(v) do
if X[u] = 0 & T[u] > T[v] + C[v, u] then
T[u]: = T[v] + C[v, u] {найден более короткий путь из s в u через v}
Н[u]: = v { запоминаем его }
end if
end for
t: = ; v: =0
{ поиск конца кратчайшего пути }
for u from I to p do
if X[u] = 0 & T[u] < t then
v: = u; t: = T[u] { вершина v заканчивает кратчайший путь из S}
end if
end for
if v = 0 then
stop { нет пути из s в t}
end if
if v = t then
stop { найден кратчайший путь из s в t}
end if
X[v]: = 1 { найден кратчайший путь из s в v}
goto M

ЗАМЕЧАНИЕ

Для применимости алгоритма Дейкстры достаточно выполнения более слабого условия, чем положительность длин дуг. А именно, достаточно выполнения неравенства треугольника: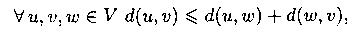

которое, очевидно, выполняется, если длины дуг неотрицательны.
обоснование
Для доказательства корректности алгоритма Дейкстры достаточно заметить, что при каждом выполнении тела цикла, начинающегося меткой М, в качестве v используется вершина, для которой известен кратчайший путь из вершины s. Другими словами, если X[v] = 1, то T[v] = d(s, v), и все вершины на пути <s, v>, определяемом вектором Н, обладают тем же свойством, то есть

Действительно (по индукции), первый раз в качестве v используется вершина s, для которой кратчайший путь пустой и имеет длину 0 (непустые пути не могут быть короче, потому что длины дуг неотрицательны). Пусть Т[u] = d(s, u) для всех ранее помеченных вершин u. Рассмотрим вновь помеченную вершину v, которая выбрана из условия

Заметим, что если известен путь, проходящий через помеченные вершины, то тем самым известен кратчайший путь. Допустим (от противного), что T[v] > d(s, v), то есть найденный путь, ведущий из s в v. не является кратчайшим. Тогда на этом пути должны быть непомеченные вершины. Рассмотрим первую вершину w на этом пути, такую что T[w] = 0. Имеем: T[w] = d(s, w) <= d(s, v) < T[v], что противоречит выбору вершины v.

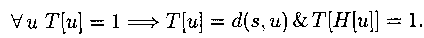
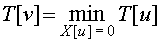
ЗАМЕЧАНИЕ

Известно, что алгоритм Флойда примерно на 50% менее трудоемок, чем применение алгоритма Дейкстры для всех пар вершин.

Упражнения

1. "Задача о гареме". Имеется конечное множество юношей, каждый из которых знаком с некоторым конечным подмножеством множества девушек. Каждый юноша желает взять в жены более чем одну знакомую девушку. Найти необходимое и достаточное условия решения этой задачи.
2. Пусть в сети G(V,E) помимо пропускной способности дуг заданы пропускные способности узлов, то есть задана нагрузка на вершины D: V R+. Для допустимого потока сумма потоков через входящие дуги не должна превышать пропускной способности вершины

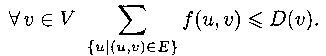
Найти максимальный поток в такой сети.
3. Пусть в графе G(V, E) заданы вероятности успешного прохождения дуг, 0 <= P[v] <= 1. Вероятность успешного прохождения пути определяется как произведение вероятностей составляющих его дуг. Построить алгоритм нахождения наиболее надежного (то есть имеющего наибольшую вероятность) пути от вершины s к вершине t.

[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]