
[Список тем] [Вступление к этой теме] Страницы темы: [1] [2]
Надежность электронных устройств по мере их совершенствования все время возрастает, но, тем не менее, в их работе возможны ошибки, как систематические, так и случайные. Сигнал в канале связи может быть искажен помехой, поверхность магнитного носителя может быть повреждена, в разъеме может быть потерян контакт. Ошибки аппаратуры ведут к искажению или потере передаваемых или хранимых данных. При определенных условиях, некоторые из которых рассматриваются в этом разделе, можно применять методы кодирования, позволяющие правильно декодировать исходное сообщение, несмотря на ошибки в данных кода. В качестве исследуемой модели достаточно рассмотреть канал связи с помехами, потому что к этому случаю легко сводятся остальные. Например, запись на диск можно рассматривать как передачу данных в канал, а чтение с диска — как прием данных из канала.
Пусть имеется канал связи С, содержащий источник помех:

где S — множество переданных, а S' — соответствующее множество принятых по каналу сообщений. Кодирование F, обладающее таким свойством, что

называется помехоустойчивым, или самокорректирующимся, или кодированием с исправлением ошибок.
Без ограничения общности можно считать, что А = В = {0, 1}, и что содержательное кодирование выполняется на устройстве, свободном от помех.
Ошибки в канале могут быть следующих типов:
 1, 1
1, 1 0 — ошибка типа замещения разряда;
0 — ошибка типа замещения разряда; 
 , 1
, 1
 — ошибка типа выпадения разряда;
— ошибка типа выпадения разряда; 
 1,
1, 
 0 — ошибка типа вставки разряда.
0 — ошибка типа вставки разряда.
Канал характеризуется верхними оценками количества ошибок каждого типа, которые возможны при передаче через канал сообщения определенной длины. Общая характеристика ошибок канала (то есть их количество и типы) обозначается
 .
.
Пример
Допустим, что имеется канал с характеристикой  = <1, 0, 0>, то есть в канале возможна одна ошибка типа замещения разряда при передаче сообщения длины n. Рассмотрим следующее кодирование: F(а): = ааа (то есть каждый разряд в сообщении утраивается) и декодирование F-1 (аbс) : = а + b + с > 1 (то есть разряд восстанавливается методом “голосования”). Это кодирование кажется помехоустойчивым для данного канала, однако на самом деле это не так. Дело в том, что при передаче сообщения длины Зn возможно не более 3 ошибок типа замещения разряда, но места этих ошибок совершенно не обязательно распределены равномерно по всему сообщению. Ошибки замещения могут произойти в соседних разрядах, и метод голосования восстановит разряд неверно.
= <1, 0, 0>, то есть в канале возможна одна ошибка типа замещения разряда при передаче сообщения длины n. Рассмотрим следующее кодирование: F(а): = ааа (то есть каждый разряд в сообщении утраивается) и декодирование F-1 (аbс) : = а + b + с > 1 (то есть разряд восстанавливается методом “голосования”). Это кодирование кажется помехоустойчивым для данного канала, однако на самом деле это не так. Дело в том, что при передаче сообщения длины Зn возможно не более 3 ошибок типа замещения разряда, но места этих ошибок совершенно не обязательно распределены равномерно по всему сообщению. Ошибки замещения могут произойти в соседних разрядах, и метод голосования восстановит разряд неверно.
Пусть E s — множество слов, которые могут быть получены из слова s в результате всех возможных комбинаций допустимых в канале ошибок
s — множество слов, которые могут быть получены из слова s в результате всех возможных комбинаций допустимых в канале ошибок
 , то есть s
, то есть s
 S
S  А*, Е
А*, Е s
s  В*. Если s'
В*. Если s'
 Е
Е s, то та конкретная последовательность ошибок, которая позволяет получить из слова s слово s', обозначается Е
s, то та конкретная последовательность ошибок, которая позволяет получить из слова s слово s', обозначается Е <s, s'>. Если тип возможных ошибок в канале подразумевается, то индекс
<s, s'>. Если тип возможных ошибок в канале подразумевается, то индекс  не указывается.
не указывается.
| Теорема |
|---|
Чтобы существовало помехоустойчивое кодирование с исправлением всех ошибок, необходимо и достаточно, чтобы s1, s2 s1, s2  S Еs1 S Еs1 Е s2 = Е s2 =  , то есть необходимо и достаточно, чтобы существовало разбиение множества В* на множества Вs ( , то есть необходимо и достаточно, чтобы существовало разбиение множества В* на множества Вs (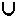 Вs = В*, Вs = В*,  Bs =
Bs =  ), такое что ), такое что s
s  S Еs S Еs  Вs.
Вs. |
Доказательство
Если кодирование помехоустойчивое, то очевидно, что Еs1
 Е s2 =
Е s2 =  . Обратно: по разбиению (
. Обратно: по разбиению (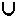 Вs строится функция F-1:
Вs строится функция F-1:
 s'
s'  F-1(s') := s'.
F-1(s') := s'.
Пример
Рассмотрим канал, в котором в любом передаваемом разряде происходит ошибка типа замещения с вероятностью р (0 < р < 1/2), причем замещения различных разрядов статистически независимы. Такой канал называется двоичным симметричным. В этом случае любое слово s  Еn2 может быть преобразовано в любое другое слово s'
Еn2 может быть преобразовано в любое другое слово s'  Еn2 замещениями разрядов. Таким образом,
Еn2 замещениями разрядов. Таким образом, s Еs = Еn2, и исправить все ошибки в двоичном симметричном канале невозможно.
s Еs = Еn2, и исправить все ошибки в двоичном симметричном канале невозможно.
Неотрицательная функция d(х, у): М х М  R+ называется расстоянием (или метрикой) на множестве М, если выполнены следующие условия (аксиомы метрики):
R+ называется расстоянием (или метрикой) на множестве М, если выполнены следующие условия (аксиомы метрики):
 х = у,
х = у,
Пусть

Эта функция называется расстоянием Хэммипга.
Мы рассматриваем симметричные ошибки, то есть если в канале допустима ошибка 0  1, то допустима и ошибка 1
1, то допустима и ошибка 1  0.
0.
Введенная функция d является расстоянием. Действительно:
является расстоянием. Действительно:
 (
(
 ',
',  ') = 0
') = 0  ' =
' =  ", поскольку ошибки симметричны, и из последовательности Е<
", поскольку ошибки симметричны, и из последовательности Е< ',
',  "> можно получить последовательность Е<
"> можно получить последовательность Е< ",
",  '>, применяя обратные ошибки в обратном порядке.
'>, применяя обратные ошибки в обратном порядке.
 (
( ',
',  ") = d
") = d (
( ",
",  ") по той же причине.
") по той же причине.
 (
( ',
',  ")<= d
")<= d (
( ',
',  ") + d
") + d (
( ",
",  '), поскольку E<
'), поскольку E< ',
',  "'>
"'> 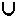 E<
E<
 '",
'",  "> является
некоторой последовательностью, преобразующей
"> является
некоторой последовательностью, преобразующей
 ' в
' в
 ", а
d
", а
d (
( ',
',
 ")
является кратчайшей из таких последовательностей.
")
является кратчайшей из таких последовательностей.
Пусть  = <аi
= <аi 
 i>ni=1 — схема некоторого алфавитного
кодирования, а d — некоторая метрика на В*. Тогда минимальное расстояние между
элементарными кодами
i>ni=1 — схема некоторого алфавитного
кодирования, а d — некоторая метрика на В*. Тогда минимальное расстояние между
элементарными кодами

называется кодовым расстоянием схемы
 .
.
| Теорема |
|---|
Алфавитное кодирование со схемой  = <аi = <аi   i>ni=1 и с кодовым расстоянием i>ni=1 и с кодовым расстоянием
является кодированием с исправлением р ошибок типа |
Доказательство
Е(х) — это шар радиуса р с центром в x для канала, который допускает не более р ошибок типа  . Таким образом,
. Таким образом,

по теореме.
Пример
Расстояние Хэмминга в 
Рассмотрим построение кода Хэмминга, который позволяет исправлять одиночные ошибки типа замещения.
Очевидно, что для исправления ошибки вместе с основным сообщением нужно передавать какую-то дополнительную информацию.
Пусть сообщение α = а1 ... аm кодируется словом  = b1 ... bn, n > m. Обозначим k: = n - m. Пусть канал допускает не более одной ошибки типа замещения в слове длины n.
= b1 ... bn, n > m. Обозначим k: = n - m. Пусть канал допускает не более одной ошибки типа замещения в слове длины n.
| Отступление |
|---|
|
Рассматриваемый случай простейший, но одновременно практически очень важный. Таким свойством, как правило, обладают внутренние шины передачи данных в современных компьютерах. |
При заданном n количество дополнительных разрядов k подбирается таким образом, чтобы 2k >= n + 1. Имеем:

Пример
Для сообщения длиной m = 32 потребуется k = 6 дополнительных разрядов, поскольку 64 = 26 > 32 + 6 + 1 = 39.
Определим последовательности натуральных чисел в соответствии с их представлениями в двоичной системе счисления следующим образом:
и т. д. По определению последовательность Vk начинается с числа 2k-1.
Рассмотрим в слове b1 ... bn k разрядов с номерами 20 = 1, 21 = 2, 22 = 4, ... 2k-1. Эти разряды назовем контрольными. Остальные разряды, а их ровно m, назовем информационными. Поместим в информационные разряды все разряды слова a1 ... аn как они есть. Контрольные разряды определим следующим образом:
 b5
b5  b7
b7  …, — то есть все разряды с номерами из V1, кроме первого;
…, — то есть все разряды с номерами из V1, кроме первого;
 b6
b6  b7
b7 
 b6
b6  b7
b7 
 и вообще,
и вообще,
Пусть после прохождения через канал получен код с1 ...
сn, то есть с1 ... сn : = С(b1 ... bn), причем

Здесь I — номер разряда, в котором, возможно, произошла ошибка замещения. Пусть это число имеет следующее двоичное представление: I = il ... i1. Определим число J = jl ... j1 следующим образом:
 c3
c3  c5
c5  c7
c7  ..., — то есть все разряды с номерами из V1;
..., — то есть все разряды с номерами из V1;
 c3
c3  c6
c6  c7
c7  ..., — то есть все разряды с номерами из V2;
..., — то есть все разряды с номерами из V2;
 c5
c5  c6
c6  c7
c7  ..., — то есть все разряды с номерами из V3;
..., — то есть все разряды с номерами из V3;и вообще,

| Теорема |
|---|
|
I=J. |
Доказательство
Эти числа равны, потому что поразрядно равны их двоичные представления.
Действительно, пусть i1 = 0. Тогда I  V1, и значит,
V1, и значит,

по определению разряда b1. Пусть теперь i1
= 1. Тогда I  V1, и значит,
V1, и значит,

так как если в сумме по модулю два изменить ровно один разряд, то изменится и
значение всей суммы. Итак, i1 = j1. Аналогично
(используя последовательности V2 и т. д.) имеем
i2 = j2 и т. д.
Таким образом, I = J.
Отсюда вытекает метод декодирования с исправлением ошибки: нужно вычислить
число J. Если J = 0, то ошибки нет, иначе сJ =
 сJ. После этого из исправленного сообщения извлекаются
информационные разряды, которые уже не содержат ошибок.
сJ. После этого из исправленного сообщения извлекаются
информационные разряды, которые уже не содержат ошибок.
[Список тем] [Вступление к этой теме] Страницы темы: [1] [2]