[Список тем]
Понятие об М-методе (методе искусственного базиса).
Выше был изложен алгоритм получения допустимого базисного решения в случае,
когда первоначальное базисное решение недопустимо. Однако при расчете с
помощью симплексных таблиц удобнее пользоваться так называемым
М-методом, или методом искусственного базиса.
Он заключается в следующем.
В каждое уравнение, дающее отрицательную компоненту в базисном решении,
вводим свою новую неотрицательную искусственную переменную
у1, у2, ..., уk,
которая имеет тот же знак, что и свободный член в правой части уравнения.
В первой таблице включаем в число основных все искусственные переменные и
те обычные выравнивающие переменные, которые определяют неотрицательные
компоненты базисного решения.
Составляем новую линейную функцию
Т = F - М(у1 + у2 + ... + уk), где М - произвольно большое число, и ищем ее максимум (T-задача). Назовем М-функцией выражение М(у1 + у2 + ... + уk).
Справедлива теорема (доказательство здесь не приводится):
| Внимание! |
|---|
1. Если в оптимальном решении Т-задачи все искусственные переменные
равны 0, то соответствующие значения остальных переменных дают
оптимальное решение исходной задачи (т.е. Tmax = Fmax, если
у1= у2 ... уk = 0
т. е. минимум М-функции равен 0).
2. Если имеется оптимальное решение Т-задачи, в котором хотя бы одна из
искусственных переменных отлична от 0, то система ограничений исходной задачи
несовместна.
3. Если Tmax = 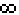 , то исходная задача также неразрешима, причем либо
Fmax =
, то исходная задача также неразрешима, причем либо
Fmax = 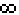 либо условия задачи противоречивы.
либо условия задачи противоречивы.
|
Из теоремы следует, что вначале следует найти минимум M-функции.
Если он равен 0 и все искусственные переменные обращаются в 0, то далее можно
отбросить эти переменные и решать исходную задачу, исходя из полученного
допустимого базисного решения. На практике находят не минимум M-функции,
а максимум (-M)-функции.
Задача 5.11 |
Решить задачу 5.3 M-методом, используя симплексные таблицы.
F = x1 + 2 x2
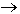 max при ограничениях:
max при ограничениях:
x1 - x2 <= -1,
x1 - x2 >= -3,
x1 <= 3,
Решение. Введем необходимое число искусственных переменных и столько же
дополнительных строк в симплексной таблице.
Имеем:
x1 - x2 + x3 = -1,
x1 - x2 - x4 = -3,
x1 + x5 = 3,
X1 = (0, 0, -1, 3, 3) - недопустимое базисное решение.
Вводим в первое уравнение искусственную переменную y1 с тем же
знаком, что и свободный член
x1 - x2 + x3 - y1 = -1,
x1 - x2 - x4 = -3,
x1 + x5 = 3,
T = x1 + 2x2 - My1
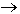 max. max.
Умножаем уравнения с отрицательной правой частью на -1. Составляем первую
симплексную таблицу
Таблица 5.5
| Базис |
Свободный
член |
Переменные |
Оценочное
Отношение |
| x1 | x2 |
x3 | х4 | x5 |
y1 |
| y1 | 1 | -1 | 1 |
-1 | 0 | 0 | 1 | 1 ¬ |
| х4 | 3 | -1 | 1 |
0 | 1 | 0 | 0 | 3 |
| x5 | 3 | 1 | 0 |
0 | 0 | 1 | 0 | 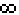
|
| F | 0 | -1 | -2 |
0 | 0 | 0 | 0 | max |
| Мф | -M | М | -М |
M | 0 | 0 | -M | max |
Последняя строка - это (-M)-функция, т.е. (-Мф)у1.
Заполняем ее, умножая строку у1 на коэффициент (-М).
Если искусственных переменных yi несколько, то заполнение
производится суммой коэффициентов столбца из всех строк с уi,
умноженной на (-М).
Проверяя выполнение критерия оптимальности при отыскании максимума
(-M)-функции, определяем, что в последней строке имеется отрицательный
элемент во втором столбце; значит он является разрешающим, переменная
х2 переходит в основные. Минимальное оценочное отношение в
первой строке, она разрешающая. Переменная у1 переходит
в неосновные, обращается в 0 на следующем базисном решении и далее исключается
из рассмотрения.
В соответствии с общим алгоритмом получаем табл. 5.6.
| Базис |
Свободный
член |
Переменные |
Оценочное
отношение |
| x1 | x2 | x3 |
х4 | x5 |
| x2 | 1 | -1 | 1 | -1 |
0 | 0 | |
| x4 | 2 | 0 | 0 | 1 |
1 | 0 | |
| x5 | 3 | 1 | 0 |
0 | 0 | 1 | |
| F | 2 | -3 | 0 | -2 |
0 | 0 | max |
| -Mф | 0 | 0 | 0 | 0 | 0 |
0 | max |
Последняя строка показывает, что критерий оптимальности выполнен; max
(-Мф) = 0, значит min Мф = 0, далее эту строку можно не
рассматривать. Получено допустимое базисное решение (0; 1; 0; 2; 3),
начиная с которого решаем исходную задачу в соответствии с обычным алгоритмом.
Завершите ее самостоятельно.
|
| Замечание |
|---|
|
При решении задачи на отыскание минимума линейной функции цели рекомендуется
вместо Zmin находить (-Z)max.
|
[Список тем]
[В начало страницы]
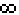 , то исходная задача также неразрешима, причем либо
Fmax =
, то исходная задача также неразрешима, причем либо
Fmax = 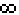 либо условия задачи противоречивы.
либо условия задачи противоречивы.
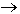 max при ограничениях:
max при ограничениях: