Преобразование выполним в два этапа. Вначале построим ДНФ, а затем
преобразуем ее в СДНФ.
Преобразование выполним в два этапа. Вначале построим КНФ, а затем
преобразуем ее в СКНФ.
| Вычисления |
Выполняемые действия |
Применяемые законы логики |
( a
a 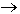  b) b)
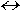 (a&
(a& c)= c)= |
Избавляемся от импликации |
x 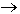 y = y =  x x
 y y |
=(a   b) b)
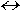 (a&
(a& c)= c)= |
Избавляемся от равнозначности |
x 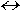 y
= (x y
= (x 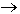 y) & (y y) & (y 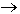 x) x) |
=(a   b b
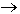 a& a& c)
&(a& c)
&(a& c c  a
a   b)= b)= |
Избавляемся от импликаций |
x  y
= y
=  x x y y
|
=( (a (a  b) b)
 a& a& c)&( c)&(
 (a& (a& c)
c) a a  b)= b)= |
Вносим отрицание в скобки |
 (x (x y)= y)= x& x& y y |
=( a&b) a&b)  a& a&
 c)&( c)&( (a& (a&
 c) c) a a  b)= b)= |
Вносим отрицание в скобки |
 (x&y) = (x&y) =
 x x  y y |
=( a&b a&b  a&
a& c)&( c)&( a a c c
 a a  b)= b)= |
Избавляемся от правых скобок
|
( a a  a)=1; x&1=x
a)=1; x&1=x |
= a & b a & b
 a&
a& c -
начальная форма соответствует здесь ДНФ. Она используется для получения СДНФ и
СКНФ c -
начальная форма соответствует здесь ДНФ. Она используется для получения СДНФ и
СКНФ |
Добавляем в ДНФ в каждую элементарную
конъюнкцию все недостающие аргументы функции со
всеми возможными сочетаниями знаков |
x = x&y  x&
x& y y |
=( a&b&c) a&b&c)
 (
( a&b& a&b& c) c)
 (a&b&
(a&b& c) c)  (a&
(a& b& b& c)
получена СДНФ c)
получена СДНФ |
|
|
 a&b a&b  a& a&
 c=( c=( a&b a&b a)
&( a)
&( a&b a&b
 c)= c)= |
К начальной форме дважды применим
дистрибутивный закон |
x  (y
& z)=(x (y
& z)=(x y) &(x y) &(x z) z) |
= ( a a a)&(a a)&(a b)&( b)&( a a
  c)&(b c)&(b
  c)= c)= |
избавляемся от умножения на 1 |
 x x x =
1; x&1= x x =
1; x&1= x |
= (a b)&( b)&( a a  c)&(b c)&(b
  c) - КНФ c) - КНФ |
Добавляем в КНФ в каждую элементарную
дизъюнкцию все недостающие аргументы функции со
всеми возможными сочетаниями знаков |
x=(x y)&(x y)&(x
 y) y) |
(a  b b  c) &
(a c) &
(a b b  c) &
( c) &
( a a b b  c) &
( c) &
( a a
 b b  c)
& (a c)
& (a  b b   c) &
( c) &
( a a  b b  c)= c)= |
2й и 5й, 4й и 6й сомножители - совпадают.
Оставляем по одному. |
x&x = x |
= (a  b b  c) & (a c) & (a b b  c)
& ( c)
& ( a a b b  c) &
( c) &
( a a  b b
  c) получена СКНФ c) получена СКНФ |
|
|
 ,
причем знак отрицания может стоять только при переменных.
,
причем знак отрицания может стоять только при переменных.
 Y) и вновь применить
преобразование (2).
Y) и вновь применить
преобразование (2). Y)
(осн.равн. 13)
Y)
(осн.равн. 13)
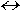 (a&
(a& y
y