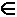 P2. Замыканием F (обозначается [F])
называется множество всех булевых функций, реализуемых формулами над F:
P2. Замыканием F (обозначается [F])
называется множество всех булевых функций, реализуемых формулами над F:[F]:= {f
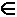 P2 | f = func T[F]}
P2 | f = func T[F]}Свойства замыкания:
Пусть F = {f1,...fm}, где fi
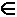 P2. Замыканием F (обозначается [F])
называется множество всех булевых функций, реализуемых формулами над F:
P2. Замыканием F (обозначается [F])
называется множество всех булевых функций, реализуемых формулами над F:
[F]:= {f 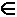 P2 | f = func T[F]}
P2 | f = func T[F]}
Свойства замыкания:
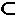 [F]
[F]
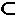 F2
→ [F1]
F2
→ [F1] 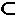 [F2 ]
[F2 ]
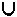 [F2]) →
[F1
[F2]) →
[F1 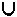 F2]
F2]
Некоторые замкнутые классы
Класс (множество) функций F называется замкнутым, если [F]=F.
Рассмотрим следующие классы функций:
 c 1x1
c 1x1 ...
...
 cnxn} т.е.
при представлении в виде многочлена Жегалкина функция не содержит произведений
переменных. Это функции f0, f10, f12, f15.
cnxn} т.е.
при представлении в виде многочлена Жегалкина функция не содержит произведений
переменных. Это функции f0, f10, f12, f15.
Каждый из этих классов функций является замкнутым и не полным.
| Теорема Поста |
|---|
| Система булевых функций F полна тогда и только тогда, когда она содержит хотя бы одну функцию, не сохраняющую 0, хотя бы одну функцию, не сохраняющую 1, хотя бы одну не самодвойственную функцию, хотя бы одну не монотонную функцию, хотя бы одну не линейную функцию т.е. система F не принадлежит ни одному из замкнутых классов. |
Система функций является полной, если с помощью ее функций можно получить все основные
логические операции {&,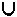 , ¬}за конечное число
действий.
, ¬}за конечное число
действий.
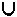 x2 =
¬(¬x1 & ¬x2);
x2 =
¬(¬x1 & ¬x2);
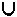 , ¬ } - полная, так как x1&x2 =
¬(¬x1
, ¬ } - полная, так как x1&x2 =
¬(¬x1 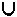 ¬x2);
¬x2);
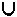 x2 = ¬(x1 ↓ x2) = (x1 ↓ x2)↓
(x1 ↓ x2);
x2 = ¬(x1 ↓ x2) = (x1 ↓ x2)↓
(x1 ↓ x2);
 } -
полная, так как ¬x= x
} -
полная, так как ¬x= x
 1. Представление функции в базисе
{0, 1, & ,
1. Представление функции в базисе
{0, 1, & ,
 } называется полиномом Жегалкина.
} называется полиномом Жегалкина.