 — бинарное отношение на Х х Y,
— бинарное отношение на Х х Y,
 —
бинарное отношение на Y x Z. Определим
композицию бинарных отношений
—
бинарное отношение на Y x Z. Определим
композицию бинарных отношений  о
о
 как бинарное отношение на Х х Z, заданное следующим:
как бинарное отношение на Х х Z, заданное следующим:x
 o
o
 z
z
 y((x
y((x y)
(y
y)
(y z)) ≡ 1
z)) ≡ 1
[Список тем] [Вступление к этой теме] Страницы темы: [1] [2]
| Определение 1 |
|---|
Пусть  — бинарное отношение на Х х Y, — бинарное отношение на Х х Y,
 —
бинарное отношение на Y x Z. Определим
композицию бинарных отношений —
бинарное отношение на Y x Z. Определим
композицию бинарных отношений  о о
 как бинарное отношение на Х х Z, заданное следующим:
как бинарное отношение на Х х Z, заданное следующим:x  o o
 z z
 y((x y((x y)
(y y)
(y z)) ≡ 1 z)) ≡ 1
|
Очевидно, что композиция ассоциативна, т. е.
( o
o  )
o
)
o 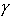

 o(
o( o
o 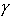 )
)
и, вообще говоря, не коммутативна, т.е. существуют
 и
и  такие, что
такие, что
 o
o  ≠
≠ o
o

Отмеченное выше соответствие между бинарными
отношениями на конечных множествах и булевыми
матрицами порождает операцию булева умножения
″0-1″ матриц. (Композиции отношений
соответствует булево произведение матриц.) Оно определено следующим правилом:
| Определение 2 |
|---|
|
Пусть А — булева матрица размера m х р с
элементами A(ij), В — булева матрица размера р х n с
элементами B(ij). Булевым произведением матриц A и В называется булева матрица A  B размера
m х n с элементами (A x B)ij, определенными равенством B размера
m х n с элементами (A x B)ij, определенными равенством
p (A  B)ij= B)ij=
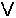 (A)ik (A)ik (B)kj (B)kjk=1 |

 B)
B)
 C = A
C = A  (B
(B  C)
C) B ≠B
B ≠B
 A
A
 o
o  ≠
≠  o
o 
 B
≠B
B
≠B  A
A
 o
o  =
=  o
o

 B=B
B=B A
A

[Список тем] [Вступление к этой теме] Страницы темы: [1] [2]