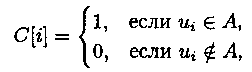
Генерирование комбинаторных объектов

Представление множеств в ЭВМ

Термин “представление” (еще употребляют термин “реализация”) применительно к программированию означает следующее. Задать представление какого-либо объекта (в данном случае множества) — значит описать в терминах используемой системы программирования структуру данных, используемую для хранения информации о представляемом объекте, и алгоритмы над выбранными структурами данных, которые реализуют присущие данному объекту операции. Предполагается, что в используемой системе программирования доступны такие общеупотребительные структуры данных, как массивы, структуры (или записи) и указатели. Таким образом, применительно к множествам определение представления подразумевает описание способа хранения информации о принадлежности элементов множеству и описание алгоритмов для вычисления объединения, пересечения и других введенных операций.
Следует подчеркнуть, что, как правило, один и тот же объект может быть представлен многими разными способами, причем нельзя указать способ, который является наилучшим для всех возможных случаев. В одних случаях выгодно использовать одно представление, а в других — другое. Выбор представления зависит от целого ряда факторов: особенностей представляемого объекта, состава и относительной частоты использования операций в конкретной задаче и т. д. Умение выбрать наиболее подходящее для данного случая представление является основой искусства практического программирования. Хороший программист отличается тем, что он знает много разных способов представления и умело выбирает наиболее подходящий.

Реализация операций над подмножествами заданного универсума U

Пусть универсум U — конечный, и число элементов в нем не превосходит разрядности ЭВМ: |U| < n. Элементы универсума нумеруются: U = {u_1,u₂..,u_n}. Подмножество А универсума U представляется кодом (машинным словом или битовой шкалой) С, в котором:

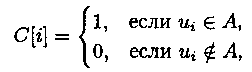
где С[i] — это i-й разряд кода С.
Код пересечения множеств A и В есть поразрядное логическое произведение кода множества А и кода множества В. Код объединения множеств А и В есть поразрядная логическая сумма кода множества А и кода множества В. Код дополнения множества А есть инверсия кода множества А. В большинстве ЭВМ для этих операций есть соответствующие машинные команды. Таким образом, операции над небольшими множествами выполняются весьма эффективно.

Замечание

Если мощность универсума превосходит размер машинного слова, но не очень велика, то для представления множеств используются массивы битовых шкал. В этом случае операции над множествами реализуются с помощью циклов по элементам массива.

Замечание
Если мощность универсума превосходит размер машинного слова, но не очень велика, то для представления множеств используются массивы битовых шкал. В этом случае операции над множествами реализуются с помощью циклов по элементам массива.

Генерация всех подмножеств универсума U

Во многих переборных алгоритмах требуется последовательно рассмотреть все подмножества заданного множества. В большинстве компьютеров целые числа представляются кодами в двоичной системе счисления, причем число 2^k — 1 представляется кодом, содержащим k единиц. Таким образом, число 0 является представлением пустого множества Ø , число 1 является представлением подмножества, состоящего из первого элемента, и т. д. Следующий тривиальный алгоритм перечисляет все подмножества n-элементного множества.

Алгоритм генерации всех подмножеств n-элементного множества

Вход: n >= 0 — мощность множества
Выход: последовательность кодов подмножеств i
for i from 0 to 2ⁿ- 1 do
yield i
end for

обоснование

Алгоритм генерации всех подмножеств n-элементного множества
Вход: n >= 0 — мощность множества Выход: последовательность кодов подмножеств i for i from 0 to 2ⁿ- 1 do yield i end for

Алгоритм выдает 2ⁿ различных целых чисел, следовательно, 2ⁿ различных кодов. С увеличением числа увеличивается количество двоичных разрядов, необходимых для его представления. Самое большое (из генерируемых) число 2ⁿ - 1 требует для своего представления ровно n разрядов. Таким образом, все подмножества генерируются, причем ровно по одному разу.
Недостаток этого алгоритма состоит в том, что порядок генераций подмножеств никак не связан с их составом. Например, вслед за подмножеством с кодом 0111 будет перечислено подмножество с кодом 1000.

Отступление

Во многих переборных задачах требуется рассмотреть все подмножества некоторого множества и найти среди них то, которое удовлетворяет заданному условию. При этом проверка условия часто может быть весьма трудоемкой и зависеть от состава элементов очередного рассматриваемого подмножества. В частности, если очередное рассматриваемое подмножество незначительно отличается по набору элементов от предыдущего, то иногда можно воспользоваться результатами оценки элементов, которые рассматривались на предыдущем шаге перебора. В таком случае, если перебирать множества в определенном порядке, можно значительно ускорить работу переборного алгоритма.

Отступление
Во многих переборных задачах требуется рассмотреть все подмножества некоторого множества и найти среди них то, которое удовлетворяет заданному условию. При этом проверка условия часто может быть весьма трудоемкой и зависеть от состава элементов очередного рассматриваемого подмножества. В частности, если очередное рассматриваемое подмножество незначительно отличается по набору элементов от предыдущего, то иногда можно воспользоваться результатами оценки элементов, которые рассматривались на предыдущем шаге перебора. В таком случае, если перебирать множества в определенном порядке, можно значительно ускорить работу переборного алгоритма.

Алгоритм построения бинарного кода Грея

Данный алгоритм генерирует последовательность всех подмножеств n-элементного множества, причем каждое следующее подмножество получается из предыдущего удалением или добавлением одного элемента.

Алгоритм построения бинарного кода Грея

Вход: n >= 0 — мощность множества
Выход: последовательность кодов подмножеств В
В : array [1..n] of 0..1 { битовая шкала для представления подмножеств }
for i from 1 to n do
B[i] := 0 { инициализация }
end for
yield В { пустое множество }
for i from 1 to 2ⁿ-1 do
p:=Q(i) { определение элемента, подлежащего добавлению или удалению }
В[р] := 1 - В[р] { добавление или удаление элемента }
yield В { очередное подмножество }
end for
proc Q(i) {количество 2 в разложении i на множители + 1 }
q := 1; j:= i
while j четно do
j := j/2; q := q+1
end while
return q
end proc

обоснование

Алгоритм построения бинарного кода Грея
Вход: n >= 0 — мощность множества Выход: последовательность кодов подмножеств В В : array [1..n] of 0..1 { битовая шкала для представления подмножеств } for i from 1 to n do B[i] := 0 { инициализация } end for yield В { пустое множество } for i from 1 to 2ⁿ-1 do p:=Q(i) { определение элемента, подлежащего добавлению или удалению } В[р] := 1 - В[р] { добавление или удаление элемента } yield В { очередное подмножество } end for proc Q(i) {количество 2 в разложении i на множители + 1 } q := 1; j:= i while j четно do j := j/2; q := q+1 end while return q end proc

Для n = 1 искомая последовательность кодов суть 0,1. Пусть есть искомая последовательность кодов B₁,..., B₂k для n = k. Тогда последовательность кодов B₁0,..., B₂k0, B₁1,..., B₂k1 будет искомой последовательностью для n = k+1. Действительно, в B₁ 0,..., B₂k0, B₁1,..., B₂k1 имеется 2^k+1 кодов, они все различны и соседние различаются ровно в одном разряде по построению. Именно такое построение и осуществляет данный алгоритм. На нулевом шаге алгоритм выдает правильное подмножество В (пустое). Пусть за первые 2^k-1 шагов алгоритм выдал последовательность значений В.
При этом B[k + 1] = B[k +2] = • • • = В[п] = 0. На 2^k-м шаге разряд B[k + 1] изменяет свое значение с 0 на 1. После этого будет повторена последовательность изменений значений В[1..k] в обратном порядке, поскольку Q(2^k + m) = Q(2^k - m) для 0 <= т <= 2^k-1.
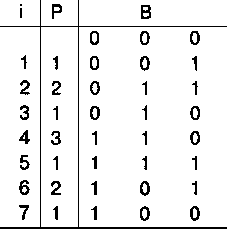
Пример
Протокол выполнения алгоритма 1.2 для n = 3.

[Список тем]