Оптимальное кодирование

[Список тем] [Вступление к этой теме] Страницы темы: [1] [2]

Оптимальное кодирование

Оптимальное кодирование обладает определенными свойствами, которые можно использовать для его построения.

ЛЕММА

Пусть = (а_i _i)ⁿ_i=1 — схема оптимального кодирования для распределения вероятностей Р = р₁ >= … > = р_n > 0. Тогда если р_i > р_j, то l_i < = l_j.

ЛЕММА
Пусть = (а_i _i)ⁿ_i=1 — схема оптимального кодирования для распределения вероятностей Р = р₁ >= … > = р_n > 0. Тогда если р_i > р_j, то l_i < = l_j.

Доказательство
От противного. Пусть i < j, р_i > р_j и l_i > 1_j. Тогда рассмотрим
' = {a₁ ₁, ..., а_i _j, ..., а_j _i, ..., а_n _n}.
Имеем:
l - l _' = (p_il_i + р_jl_j) - (p_il_j + p_jl_i) = (р_i – р_j)(l_i - l_j) > 0,
что противоречит тому, что — оптимально.
Таким образом, не ограничивая общности, можно считать, что l_i <= … <= 1_n.

ЛЕММА

Если = (а_i _i)ⁿ_i=1 — схема оптимального префиксного кодирования для распределения вероятностей Р = р₁ > = … >= р_n > 0, то среди элементарных кодов, имеющих максимальную длину, имеются два, которые различаются только в последнем разряде.

ЛЕММА
Если = (а_i _i)ⁿ_i=1 — схема оптимального префиксного кодирования для распределения вероятностей Р = р₁ > = … >= р_n > 0, то среди элементарных кодов, имеющих максимальную длину, имеются два, которые различаются только в последнем разряде.

Доказательство
От противного.

Пусть кодовое слово максимальной длины одно и имеет вид _n = b, где b = 0 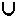b = 1. Имеем: 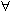_i 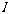1..n - 1 1_i <= | |. Так как схема префиксная, то слова ₁, ..., _n-1 не являются префиксами . С другой стороны, не является префиксом слов ₁, ..., _n-1, иначе было бы = _j, а значит, _j было бы префиксом _n. Тогда схема ':= <а₁ ₁, ..., а_n > тоже префиксная, причем l _'(Р) = l (Р) – р_n, что противоречит оптимальности .
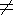
Пусть теперь два кодовых слова _n-1 и _n максимальной длины отличаются не в последнем разряде, то есть _n-1 = 'b', _n = "b", ' ", причем ', " не являются префиксами для ₁, ..., _n-2 и наоборот. Тогда схема ':= <а₁ ₁, ..., а_n-2 _n-2, а_n-1 'b', а_n "> также является префиксной, причем l_'(Р) = l (Р) – р_n, что противоречит оптимальности .

Теорема
Если _n-1 = (a_i _i)^n-1_i=1 — схема оптимального префиксного кодирования для распределения вероятностей Р = р₁ >= … >= р_n-1 > 0 и р_j = q' + q", причем р₁ >= … >= р_j-1 >= р_j+1 >= … >= р_n-1 >= q' >= q" > 0, то кодирование со схемой _n = (a₁ ₁, ..., а_j-1 _j-1, а_j+1 _j+1, ..., a_n-1 _n-1, a_j _j0, a_n _j1) является оптимальным префиксным кодированием для распределения вероятностей Р_n = p₁, ..., р_j-1, p_j+1, ..., р_n-1, q', q".

Теорема

Если _n-1 = (a_i _i)^n-1_i=1 — схема оптимального префиксного кодирования для распределения вероятностей Р = р₁ >= … >= р_n-1 > 0 и р_j = q' + q", причем
р₁ >= … >= р_j-1 >= р_j+1 >= … >= р_n-1 >= q' >= q" > 0,
то кодирование со схемой
_n = (a₁ ₁, ..., а_j-1 _j-1, а_j+1 _j+1, ..., a_n-1 _n-1, a_j _j0, a_n _j1)
является оптимальным префиксным кодированием для распределения вероятностей Р_n = p₁, ..., р_j-1, p_j+1, ..., р_n-1, q', q".

Доказательство

Если _n-1 было префиксным, то _n тоже будет префиксным по построению.
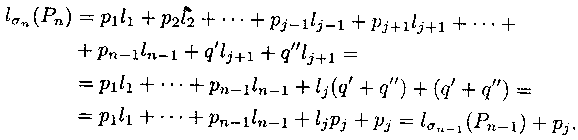
Пусть схема '_n: = {а_i _i}ⁿ_i=1 оптимальна для Р_n. Тогда по предшествующей лемме '_n = {a₁ '₁, ..., а_n-2 '_n-2, а_n-1 0, а_n 1}. Положим l' = || и рассмотрим схему '_n-1: = {а₁ '₁, ..., а_j , ..., а_n-2 '_n-2}, где j определено так, чтобы р_j-1 >= q' + q" >= р_j+1.
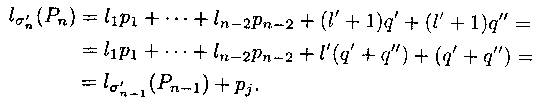
'_nn - префиксное, значит, '_n-1 тоже префиксное.
'_n - оптимально, значит, l '_n-1(Р_n-1) >= l _n-1(P_n-1).
l_n(Р_n) = l _n-1(Р_n-1) + р_j <= l'_n-1 (Р_n-1) + p_j = l'_n(Р_n), но '_n - оптимально, значит, _n оптимально.

Алгоритм Хаффмена

Следующий рекурсивный алгоритм строит схему оптимального префиксного алфавитного кодирования для заданного распределения вероятностей появления букв.

Алгоритм Хаффмена

Построение оптимальной схемы - рекурсивная процедура Huffman
Вход: n - количество букв, Р : аrrау [1..n] of real - массив вероятностей букв, упорядоченный по убыванию.
Выход: С : аrrау [1..n, 1..L] of 0..1 – массив элементарных кодов,
l: аrrау [1..n] of 1..L –массив длин элементарных кодов схемы оптимального префиксного кодирования
if n=2 then
С[1,1]:= 0; l[1]:= 1{ первый элемент }
С[2,1]:= 1; l[2]:=1{ второй элемент }
else
q:= Р[n - 1] + Р[n] { сумма двух последних вероятностей }
j:= Uр(n, q) { поиск места и вставка суммы }
Huffman (Р, n - 1) { рекурсивный вызов }
Down (n, j) { достраивание кодов }
end if

Функция Uр находит в массиве Р место, в котором должно находиться число q
(см. предыдущий алгоритм) и вставляет это число, сдвигая вниз остальные элементы.

Вход: n — длина обрабатываемой части массива Р, q — вставляемая сумма.
Выход: измененный массив Р.
for i from n-1 downto 2 do
if P[i-1] <= q then
Р[i]:= P[i-1] { сдвиг элемента массива }
else
j:= i-1 { определение места вставляемого элемента }
exit for i { все сделано — цикл не нужно продолжать }
end if
end for
Р[j]: = q { запись вставляемого элемента }
return j

Процедура Down строит оптимальный код для n букв на основе построенного оптимального кода для n - 1 буквы. Для этого код буквы с номером j временно исключается из массива С путем сдвига вверх кодов букв с номерами, большими j, а затем в конец обрабатываемой части массива С добавляется пара кодов, полученных из кода буквы с номером j удлинением на 0 и 1, соответственно. Здесь С'[i, *] означает вырезку из массива, то есть i-ю строку массива С.

Вход: n — длина обрабатываемой части массива Р, j — номер “разделяемой” буквы.
Выход: оптимальные коды в первых n элементах массивов С и l.
с:= С[j, *]{ запоминание кода буквы j }
l:= l[j] { и длины этого кода }
for i from j to n-2 do
C[i, *]:= С[i+1, *] { сдвиг кода }
l[i]:= l[i+1] { и его длины }
end for
С[n-1, *]:= с; С[n, *]:= с{ копирование кода буквы j }
С[n-1, l+1]:= 0; С[n, l+1]:= 1{ наращивание кодов }
l[n-1]:= l+1; l[n]:= l + 1{ и увеличение длин }

Алгоритм Хаффмена
Построение оптимальной схемы - рекурсивная процедура Huffman Вход: n - количество букв, Р : аrrау [1..n] of real - массив вероятностей букв, упорядоченный по убыванию. Выход: С : аrrау [1..n, 1..L] of 0..1 – массив элементарных кодов, l: аrrау [1..n] of 1..L –массив длин элементарных кодов схемы оптимального префиксного кодирования if n=2 then С[1,1]:= 0; l[1]:= 1{ первый элемент } С[2,1]:= 1; l[2]:=1{ второй элемент } else q:= Р[n - 1] + Р[n] { сумма двух последних вероятностей } j:= Uр(n, q) { поиск места и вставка суммы } Huffman (Р, n - 1) { рекурсивный вызов } Down (n, j) { достраивание кодов } end if
Функция Uр находит в массиве Р место, в котором должно находиться число q (см. предыдущий алгоритм) и вставляет это число, сдвигая вниз остальные элементы.
Вход: n — длина обрабатываемой части массива Р, q — вставляемая сумма. Выход: измененный массив Р. for i from n-1 downto 2 do if P[i-1] <= q then Р[i]:= P[i-1] { сдвиг элемента массива } else j:= i-1 { определение места вставляемого элемента } exit for i { все сделано — цикл не нужно продолжать } end if end for Р[j]: = q { запись вставляемого элемента } return j
Процедура Down строит оптимальный код для n букв на основе построенного оптимального кода для n - 1 буквы. Для этого код буквы с номером j временно исключается из массива С путем сдвига вверх кодов букв с номерами, большими j, а затем в конец обрабатываемой части массива С добавляется пара кодов, полученных из кода буквы с номером j удлинением на 0 и 1, соответственно. Здесь С'[i, ]* означает вырезку из массива, то есть i-ю строку массива С.
Вход: n — длина обрабатываемой части массива Р, j — номер “разделяемой” буквы. Выход: оптимальные коды в первых n элементах массивов С и l. с:= С[j, ]{ запоминание кода буквы j } l:= l[j]* { и длины этого кода } for i from j to n-2 do C[i, ]:= С[i+1, ] { сдвиг кода } l[i]:= l[i+1] { и его длины } end for С[n-1, ]:= с; С[n, ]:= с{ копирование кода буквы j } С[n-1, l+1]:= 0; С[n, l+1]:= 1{ наращивание кодов } l[n-1]:= l+1; l[n]:= l + 1{ и увеличение длин }

Обоснование
Для пары букв при любом распределении вероятностей оптимальное кодирование очевидно: первой букве нужно назначить код 0, а второй — 1. Именно это и делается в первой части оператора if основной процедуры Huffman. Рекурсивная часть алгоритма в точности следует доказательству теоремы предыдущего подраздела. С помощью функции Uр в исходном упорядоченном массиве Р отбрасываются две последние (наименьшие) вероятности, и их сумма вставляется в массив Р, так чтобы массив (на единицу меньшей длины) остался упорядоченным. Заметим, что при этом место вставки сохраняется в локальной переменной j. Так происходит до тех пор, пока не останется массив из двух элементов, для которого оптимальный код известен. После этого в обратном порядке строятся оптимальные коды для трех, четырех и т. д. элементов. Заметим, что при этом массив вероятностей Р уже не нужен — нужна только последовательность номеров кодов, которые должны быть изъяты из массива кодов и продублированы в конце с добавлением разряда. А эта последовательность хранится в экземплярах локальной переменной j, соответствующих рекурсивным вызовам процедуры Huffman.
Пример
Построение оптимального кода Хаффмена для n = 7. В левой части таблицы показано изменение массива Р, а в правой части — массива С. Позиция, соответствующая текущему значению переменной j, выделена полужирным начертанием.

0.20 0.20 0.23 0.37 0.40 0.60 0 1 00 01 10 10

0.20 0.20 0.20 0.23 0.37 0.40 1 00 01 10 11 11

0.19 0.19 0.20 0.20 0.23 01 10 11 000 000

0.12 0.18 0.19 0.20 11 000 001 010

0.11 0.12 0.18 001 010 011

0.09 0.11 011 0010

0.09 0011

Цена кодирования составляет
0.20 * 2 + 0.20 * 2 + 0.19 * 3 + 0.12 * 3 + 0.11 * 3 + 0.09 * 4 + 0.09 * 4 = 2.78,
что несколько лучше, чем в кодировании, полученном алгоритмом Фано.

[Список тем] [Вступление к этой теме] Страницы темы: [1] [2]

0.20	0.20	0.23	0.37	0.40	0.60	0	1	00	01	10	10
0.20	0.20	0.20	0.23	0.37	0.40	1	00	01	10	11	11
0.19	0.19	0.20	0.20	0.23			01	10	11	000	000
0.12	0.18	0.19	0.20					11	000	001	010
0.11	0.12	0.18							001	010	011
0.09	0.11									011	0010
0.09											0011