[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3] [4] [5] [6] [7] [8]

Дополнение множества

Множество X, определяемое из соотношения
Х = I \ Х, (23)
называют дополнением множества Х (до универсального множества I ). На рис. 6 множество Х представляет собой незаштрихованную область. Формальное определение
Х = {х | х I и х Х}.

Рис. 6. Дополнение множества

Пример 9 Если I={1, 2, 3, 4, 5, 6, 7} и Х={3, 5, 7}, то Х = {1,2,4,6}.
Из (23) следует, что X и X не имеют общих элементов, так что
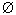X X =       (24)
Кроме того, не имеется элементов I, которые не принадлежали бы ни X, ни X, так как те элементы, которые не принадлежат X, принадлежат X. Следовательно,
Х Х=I.       (25)
Из симметрии формул (24) и (25) относительно Х и Х следует не только то, что Х является дополнением X, но и что Х является дополнением X. Но дополнение Х есть X. Таким образом,
X = X.      (26)
С помощью операции дополнения можно в удобном виде представить разность множеств
X\Y={x|x X и x Y}={x|x X и x Y},
т. е.
X \Y = X Y       (27)

Разбиение множества

Одной из наиболее часто встречающихся операций над множествами является операция разбиения множества на систему подмножеств.
Так, система курсов данного факультета является разбиением множества студентов факультета;
система групп данного курса является разбиением множества студентов курса.
Если N-множество натуральных чисел, а А₀ и А₁-множества четных и не четных чисел, то система {А₀, А₁} будет разбиением множества N.
Множество натуральных чисел может быть разбито иначе: на множество чисел, делящихся на 3 без остатка, с остатком 1 и с остатком 2.
Продукция предприятия разбивается на систему множеств, состоящих из продукции первого сорта, второго сорта и брака.
Подобные примеры можно было бы продолжать бесконечно.

Для того, чтобы дать понятию разбиения строгое определение, рассмотрим некоторое множество М и систему множеств M={X₁, ..., X_n}.

Определение
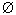Систему множеств M называют разбиением множества М, если удовлетворяются следующие условия: 1) любое множество Х из M является подмножеством множества М: Х M [ X М];       (28) 2) любые два множества Х и Y из M являются непересекающимися: X, Y M [ X ≠ Y → X Y= ];       (29) 3) объединение всех множеств, входящих в разбиение, дает множество M: Х = М.       (30) X M

К понятию разбиения мы вернемся при рассмотрении отношения эквивалентности, с которым оно очень тесно связано.

[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3] [4] [5] [6] [7] [8]