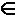 A*, то количество букв в слове называется длиной слова: α =
|а1 ... аk| = k. Пустое слово обозначается
A*, то количество букв в слове называется длиной слова: α =
|а1 ... аk| = k. Пустое слово обозначается
 :
: 
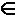 A*, |
A*, | | = 0,
| = 0,

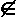 A.
A.
[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]
Кодирование F может сопоставлять код всему сообщению из множества S как единому целому или же строить код сообщения из кодов его частей. Элементарной частью сообщения является одна буква алфавита A. Этот простейший случай рассматривается в этом и следующих двух разделах.
| Определение |
|---|
| Пусть задано конечное множество А = {a1, ..., аn}, которое называется алфавитом. Элементы алфавита называются буквами. Последовательность букв называется словом (в данном алфавите). |
Множество слов в алфавите А обозначается А*. Если слово
α = a1 ... аk 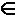 A*, то количество букв в слове называется длиной слова: α =
|а1 ... аk| = k. Пустое слово обозначается
A*, то количество букв в слове называется длиной слова: α =
|а1 ... аk| = k. Пустое слово обозначается
 :
: 
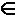 A*, |
A*, | | = 0,
| = 0,

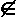 A.
A.
| Определение |
|---|
Если α = α1α2.
то α1 называется началом, или префиксом, слова
α
, а α
2 — окончанием, или постфиксом, слова α. Если при
этом α1 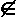  (соответственно, α2
(соответственно, α2 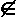
 ), то α1 (соответственно,
α2) называется собственным началом (соответственно,
собственным окончанием) слова α. ), то α1 (соответственно,
α2) называется собственным началом (соответственно,
собственным окончанием) слова α.
|
Алфавитное (или побуквенное) кодирование задается схемой (или таблицей кодов)
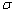 :
: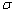 := <а1
:= <а1 
 1, ..., аn
1, ..., аn

 n>,
аi
n>,
аi 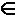 A,
A,
 i
i 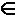 В*.
В*.
Множество кодов букв V:= {  i }
называется множеством элементарных кодов.
Алфавитное кодирование пригодно для любого множества сообщений S:
i }
называется множеством элементарных кодов.
Алфавитное кодирование пригодно для любого множества сообщений S:
F : А*  В*,
аi1 ... аik = α
В*,
аi1 ... аik = α
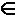 A*, F(α): =
A*, F(α): =
 i1 ...
i1 ...  ik.
ik.
Пример
Рассмотрим алфавиты A: ={0,1,2,3,4,5,6,7,8,9}, В: ={0,1} и
схему
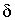 := <0
:= <0 0,
1
0,
1 1,
2
1,
2 10,
3
10,
3 11,
4
11,
4 100,
5
100,
5 101,
6
101,
6 110,
7
110,
7 111,
8
111,
8 1000,9
1000,9 1001>.
1001>.
Эта схема однозначна, но кодирование не является взаимно однозначным:
F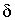 (333) = 111111 = F
(333) = 111111 = F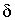 (77),
(77),
а значит, невозможно декодирование. С другой стороны, схема
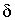 : = <0
: = <0 0000,
1
0000,
1 0001,
2
0001,
2 0010,
3
0010,
3 0011,
4
0011,
4 0100,
5
0100,
5 0101,
6
0101,
6 0110,
7
0110,
7 0111,
8
0111,
8 1000,
9
1000,
9 1001>,
1001>,
известная под названием “двоично-десятичное кодирование”, допускает
однозначное декодирование.
Рассмотрим схему алфавитного кодирования 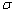 и различные слова, составленные из элементарных кодов.
и различные слова, составленные из элементарных кодов.
| Определение |
|---|
Схема 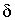 называется разделимой, если называется разделимой, если i1 ... i1 ...  ik =
ik =  j1 ... j1 ...
 jl ==>
k = l & jl ==>
k = l & 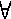 t t 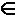 1 .. k it = jt,
1 .. k it = jt,то есть любое слово, составленное из элементарных кодов, единственным образом разлагается на элементарные коды. Алфавитное кодирование с разделимой схемой допускает декодирование. |
Если таблица кодов содержит одинаковые элементарные коды, то есть если
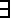 i, j i
i, j i 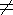 j &
j &
 i =
i =  j,
j,
где  i
i  j
j 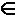 V, то схема заведомо не является
разделимой. Такие схемы далее не рассматриваются, то есть
V, то схема заведомо не является
разделимой. Такие схемы далее не рассматриваются, то есть
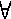 i
i 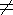 j
j
 i,
i,  j
j 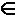 V ==>
V ==>
 i
i 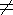
 j.
j.
| Определение |
|---|
Схема 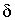 называется префиксной, если элементарный код одной буквы не является
префиксом элементарного кода другой буквы:
( называется префиксной, если элементарный код одной буквы не является
префиксом элементарного кода другой буквы:
( 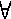 i i 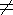 j j
 i,
i,  j j 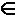 V) ==> (
V) ==> ( 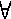 
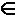 B*
B*  i i 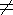
 j j ). ). |
| Теорема |
|---|
|
Префиксная схема является разделимой. |
Доказательство
От противного. Пусть кодирование со схемой а не является разделимым.
Тогда существует такое слово 
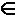 F
F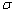 (А*), что
(А*), что
 =
=  i1 ...
i1 ...  ik, =
ik, =
 j1 ...
j1 ...  jl & (
jl & (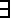 t
t 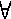 s(s < t ==>
s(s < t ==>  is =
is =  js &
js &
 it
it 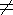
 jt)).
jt)).
Поскольку  it ...
it ...
 ik =
ik =  jt ...
jt ...
 jl, значит,
jl, значит, 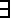
 ' (
' ( it =
it =  jt
jt  '
' 
 jt =
jt =  jt
jt  '), но это противоречит тому, что схема префиксная.
'), но это противоречит тому, что схема префиксная.
| Замечание |
|---|
| Свойство быть префиксной является достаточным, но не является необходимым для разделимости схемы. |
Пример
Разделимая, но не префиксная схема: А = {а, b}, В = {0,1},
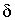 = {а
= {а  0, b
0, b
 01}.
01}.
Чтобы схема алфавитного кодирования была разделимой, необходимо, чтобы длины
элементарных кодов удовлетворяли определенному соотношению, известному как
неравенство Макмиллана.
| Теорема |
|---|
Если схема 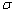 = <аi
= <аi 
 i>ni=1 разделила,
то i>ni=1 разделила,
то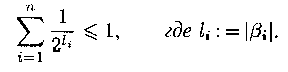 |
Доказательство
Обозначим
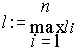
Рассмотрим n-ю степень левой части неравенства
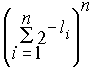
Раскрывая скобки, имеем сумму
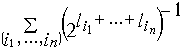
где i1, ..., in — различные наборы номеров
элементарных кодов. Обозначим через 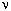 (n, t) количество входящих в эту сумму слагаемых вида 1/2t,
где t = li1 + … + lin. Для некоторых t может быть, что
(n, t) количество входящих в эту сумму слагаемых вида 1/2t,
где t = li1 + … + lin. Для некоторых t может быть, что 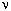 (n, t) = 0. Приводя подобные, имеем сумму
(n, t) = 0. Приводя подобные, имеем сумму
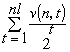
Каждому слагаемому вида (2Li1 + … + Lin)-1 можно
однозначно сопоставить код (слово в алфавите В) вида  i1 ...
i1 ...  in. Это слово состоит из п элементарных кодов и имеет длину t.
in. Это слово состоит из п элементарных кодов и имеет длину t.
Таким образом, 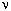 (n, t) — это число некоторых слов вида
(n, t) — это число некоторых слов вида  i1 ...
i1 ...  in, таких что |
in, таких что | i1 …
i1 … in| = t. В силу разделимости схемы
in| = t. В силу разделимости схемы 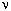 (n, t) <=
2t, в противном случае заведомо существовали бы два одинаковых
слова
(n, t) <=
2t, в противном случае заведомо существовали бы два одинаковых
слова  i1 ...
i1 ...  in =
in =  j1 ...
j1 ...  jn, допускающих различное разложение. Имеем
jn, допускающих различное разложение. Имеем
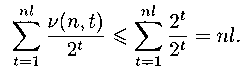
Следовательно,
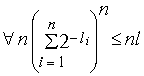
и значит,
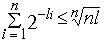 откуда
откуда
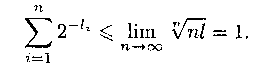
Неравенство Макмиллана является не только необходимым, но и в некотором смысле
достаточным условием разделимости схемы алфавитного кодирования.
| Теорема |
|---|
|
Если числа l1, ..., ln удовлетворяют неравенству то существует разделимая схема алфавитного кодирования
|
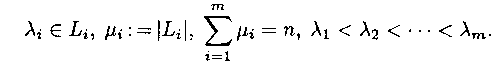
Тогда неравенство Макмиллана можно записать так:
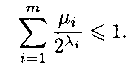
Из этого неравенства следуют т неравенств для частичных сумм:
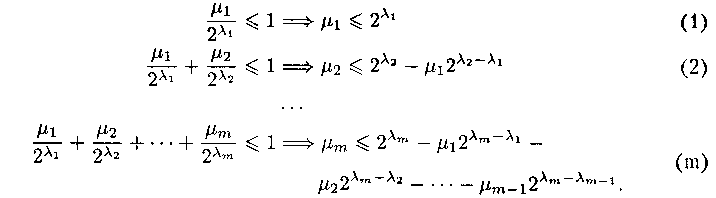
Рассмотрим слова длины  1 в алфавите В. Поскольку
1 в алфавите В. Поскольку
 1 <= 2
1 <= 2 1, из этих слов можно выбрать
1, из этих слов можно выбрать
 1 различных слов
1 различных слов
 1, ...,
1, ..., 
 1 длины
1 длины  1. Исключим из дальнейшего рассмотрения все слова из В*,
начинающиеся со слов
1. Исключим из дальнейшего рассмотрения все слова из В*,
начинающиеся со слов  1, ...,
1, ..., 
 1. Далее рассмотрим множество слов в алфавите В длиной
1. Далее рассмотрим множество слов в алфавите В длиной
 2 и не начинающихся со слов
2 и не начинающихся со слов  1, ...,
1, ..., 
 1. Таких слов будет 2
1. Таких слов будет 2 2 -
2 -  12
12 2-
2- 1. Но
1. Но  2 <= 2
2 <= 2 2 -
2 -  12
12 2-
2- 1, значит, можно выбрать
1, значит, можно выбрать  2 различных слов. Обозначим их
2 различных слов. Обозначим их 
 1+1, ...,
1+1, ..., 
 1+
1+ 2. Исключим слова, начинающиеся с
2. Исключим слова, начинающиеся с 
 1+1, ...,
1+1, ..., 
 1+
1+ 2, из дальнейшего рассмотрения. И так далее, используя неравенства для
частичных сумм, мы будем на i-м шаге выбирать
2, из дальнейшего рассмотрения. И так далее, используя неравенства для
частичных сумм, мы будем на i-м шаге выбирать
 i, слов длины
i, слов длины
 i,
i, 
 1+
1+ 2+…+
2+…+ i-1, ...,
i-1, ..., 
 1+
1+ 2+…+
2+…+ i-1+
i-1+ i, причем эти слова не будут начинаться с тех слов, которые были выбраны
раньше. В то же время длины этих слов все время растут (так как
i, причем эти слова не будут начинаться с тех слов, которые были выбраны
раньше. В то же время длины этих слов все время растут (так как
 1 <
1 <  2 < … <
2 < … <  m), поэтому они не могут быть префиксами тех слов, которые выбраны
раньше. Итак, в конце имеем набор из n слов
m), поэтому они не могут быть префиксами тех слов, которые выбраны
раньше. Итак, в конце имеем набор из n слов  1, ...,
1, ..., 
 1+…+
1+…+ m =
m =  n, |
n, | 1| = l1, …, |
1| = l1, …, | n| = ln, коды
n| = ln, коды  1, ...,
1, ...,  n не являются префиксами друг друга, а значит, схема
n не являются префиксами друг друга, а значит, схема
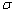 = <аi
= <аi 
 i>ni=1 будет префиксной и, по теореме
предыдущего подраздела, разделимой.
i>ni=1 будет префиксной и, по теореме
предыдущего подраздела, разделимой.
Пример:
Азбука Морзе — это схема алфавитного кодирования
<А 01, В
01, В 1000, С
1000, С 1010, D
1010, D 100, Е
100, Е 0, F
0, F 0010, G
0010, G 110, Н
110, Н 0000, I
0000, I 00, J
00, J 0111, К
0111, К 101, L
101, L 0100, М
0100, М 11, N
11, N 10, О
10, О 111, Р
111, Р 0110, Q
0110, Q 1101, R
1101, R 010, S
010, S 000, T
000, T 1, U
1, U 001, V
001, V 0001, W
0001, W 011, Х
011, Х 1001, Y
1001, Y 1011, Z
1011, Z 1100>,
1100>,
где по историческим и техническим причинам 0 называется точкой и обозначается
знаком ″.″, а 1 называется тире и обозначается знаком “—”. Имеем:
1/4 + 1/16 + 1/16 + 1/8 + 1/2 + 1/16 + 1/8 + 1/16 + 1/4 + 1/16 + 1/8 + 1/16 + 1/4 + 1/4 + 1/8 + 1/16 + 1/16 + 1/8 + 1/8 + 1/2 + 1/8 + 1/16 + 1/8 + 1/16 + 1/16 + 1/16 = 2/2 + 4/4 + 7/8 + 12/16 = 3 + 5/8 > 1.
Таким образом, неравенство Макмиллана для азбуки Морзе не выполнено, и эта
схема не является разделимой. На самом деле в азбуке Морзе имеются
дополнительные элементы — паузы между буквами (и словами), которые позволяют
декодировать сообщения. Эти дополнительные элементы определены неформально,
поэтому прием и передача сообщений с помощью азбуки Морзе, особенно с высокой
скоростью, является некоторым искусством, а не простой технической процедурой.
[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]