[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
[3]
Кодирование с минимальной избыточностью
Для практики важно, чтобы коды сообщений имели по возможности наименьшую длину.
Алфавитное кодирование пригодно для любых сообщений, то есть S = А*.
Если больше про множество S ничего не известно, то точно сформулировать
задачу оптимизации затруднительно. Однако на практике часто доступна
дополнительная информация. Например, для текстов на естественных языках
известно распределение вероятности появления букв в сообщении. Использование
такой информации позволяет строго поставить и решить задачу построения
оптимального алфавитного кодирования.
1. Минимизация длины кода сообщения
Если задана разделимая схема алфавитного кодирования
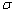 = <аi
= <аi 
 i>ni=1, то любая
схема
i>ni=1, то любая
схема
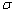 ' = <аi
' = <аi 
 'i>ni=1, где <
'i>ni=1, где < '1, ...,
'1, ...,  'n> является перестановкой <
'n> является перестановкой < 1, ...,
1, ...,  n>. также будет разделимой. Если длины элементарных кодов равны,
то перестановка элементарных кодов в схеме не влияет на длину кода сообщения.
Но если длины элементарных кодов различны, то длина кода сообщения зависит от
состава букв в сообщении и от того, какие элементарные коды каким буквам
назначены.
n>. также будет разделимой. Если длины элементарных кодов равны,
то перестановка элементарных кодов в схеме не влияет на длину кода сообщения.
Но если длины элементарных кодов различны, то длина кода сообщения зависит от
состава букв в сообщении и от того, какие элементарные коды каким буквам
назначены.
Если заданы конкретное сообщение и конкретная схема кодирования, то нетрудно
подобрать такую перестановку элементарных кодов, при которой длина кода
сообщения будет минимальна.
Пусть k1, ..., kn — количества вхождений букв
a1, ..., аn в сообщение S, а
l1, ..., ln — длины элементарных кодов
 1, ...,
1, ...,
 n, соответственно. Тогда, если
ki <= kj и l1 >=
lj, то kili +
kjlj <= kilj +
kjli.
n, соответственно. Тогда, если
ki <= kj и l1 >=
lj, то kili +
kjlj <= kilj +
kjli.
Действительно, пусть kj = k + а, ki =
k и lj = l, li = l + b, где а, b
>= 0. Тогда
(kilj + kjli) -
(kili + kjlj) = (kl +
(k + а)(l + b)) - (k(l + b) + l(k + а)) = (kl + аl + bk + аb + kl) -
(kl + аl + kl + bk) = аb >= 0.
Отсюда вытекает алгоритм назначения элементарных кодов, при котором длина
кода конкретного сообщения S будет минимальна: нужно отсортировать
буквы в порядке убывания количества вхождений, элементарные коды отсортировать
в порядке возрастания длины и назначить коды буквам в этом порядке.
Этот простой метод решает задачу минимизации длины кода только для
фиксированного сообщения S и фиксироваиной схемы
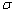 .
.
2. Цена кодирования
Пусть заданы алфавит А = {a1, ..., аn} и
вероятности появления букв в сообщении Р = <р1, ...,
рn> (рi — вероятность появления буквы
аi). Не ограничивая общности, можно считать, что
рi + ... + рn = 1 и р1 >= ...
>= рn > 0 (то есть можно сразу исключить буквы, которые
не могут появиться в сообщении, и упорядочить буквы по убыванию вероятности
их появления).
Пример
Для разделнмой схемы А = {а, b}, В = {0, 1},
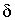 = {а
= {а  0, b
0, b
 01} при распределении
вероятностей <0.5, 0.5> цена кодирования составляет 0.5 * 1 + 0.5 *
2 = 1.5, а при распределении вероятностей <0.9, 0.1> она равна 0.9 *
1 + 0.1 * 2 = 1.1.
01} при распределении
вероятностей <0.5, 0.5> цена кодирования составляет 0.5 * 1 + 0.5 *
2 = 1.5, а при распределении вероятностей <0.9, 0.1> она равна 0.9 *
1 + 0.1 * 2 = 1.1.
Обозначим
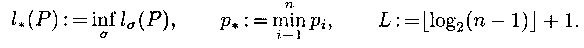
Очевидно, что всегда существует разделимая схема 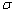 = (аi
= (аi

 i)ni=1,
такая что
i)ni=1,
такая что 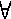 i |
i | i|
= L. Такая схема называется схемой равномерного кодирования. Следовательно,
1 <= l*(Р) <= L и достаточно учитывать только такие
схемы, для которых
i|
= L. Такая схема называется схемой равномерного кодирования. Следовательно,
1 <= l*(Р) <= L и достаточно учитывать только такие
схемы, для которых 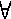 i рili
<= L, где li — целое и li <=
L/р*. Таким образом, имеется лишь конечное число схем
i рili
<= L, где li — целое и li <=
L/р*. Таким образом, имеется лишь конечное число схем
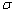 , для которых l*(Р) <=
l
, для которых l*(Р) <=
l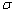 (Р) <= L. Следовательно, существует схема
(Р) <= L. Следовательно, существует схема
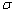 *, на которой инфимум достигается:
l
*, на которой инфимум достигается:
l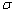 *(Р) = l*(Р).
*(Р) = l*(Р).
Алфавитное (разделимое) кодирование 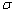 *
для которого l
*
для которого l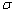 *(Р) =
l*(Р), называется кодированием с минимальной
избыточностью, или оптимальным кодированием, для распределения
вероятностей Р.
*(Р) =
l*(Р), называется кодированием с минимальной
избыточностью, или оптимальным кодированием, для распределения
вероятностей Р.
3. Алгоритм Фано
Следующий рекурсивный алгоритм строит разделимую префиксную схему алфавитного
кодирования, близкого к оптимальному.
| Алгоритм построения кодирования, близкого к
оптимальному |
|---|
Вход: Р : аrrау [1..n] оf rеаl — массив
вероятностей появления букв в сообщении, упорядоченный по невозрастанию; 1
>= Р[1] >= … >= Р[n] > 0, Р[1] + …+ Р[n] = 1.
Выход: С : аrrау [1..n, 1..L] оf 0..1 —
массив элементарных кодов.
Fаnо (1, n, 0) { вызов рекурсивной процедуры Fаnо }
Основная работа по построению элементарных кодов выполняется следующей
рекурсивной процедурой Fаnо.
Вход: b — индекс начала обрабатываемой части массива Р,
е — индекс конца обрабатываемой части массива Р, k — длина уже
построенных кодов в обрабатываемой части массива С.
Выход: заполненный массив С.
if e>b then
k: = k + 1 { место для очередного разряда в коде }
m: = Меd (b, е) { деление массива на две части }
for i from b to e do
С[i, k]: = i > m { в первой части добавляем 0, во второй — 1 }
end for
Fаnо(b, m, k) { обработка первой части }
Fаnо(m + 1, е, k) { обработка второй части }
end if
Функция Меd находит медиану указанной части массива Р[b..е], то есть определяет такой индекс m (b <= m < е), что сумма элементов Р[b..m] наиболее близка к сумме элементов Р[m + 1..е].
Вход: b — индекс начала обрабатываемой части массива Р, е — индекс конца обрабатываемой части массива Р.
Выход: m — индекс медианы, то есть
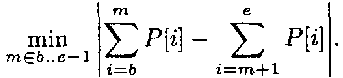
Sb:= 0 { сумма элементов первой части }
for i from b to e-1 do
Sb:= Sb + Р[i] { вначале все, кроме последнего }
end for
Sе:= Р[е] { сумма элементов второй части }
m:= е { начинаем искать медиану с конца }
repeat
d:= Sb - Sе { разность сумм первой и второй части }
m:= m - 1 { сдвигаем границу медианы вниз }
Sb:= Sb - Р[m]; Se:= Sе + Р[m]
until |Sb - Se| >=
d
return m
|
Обоснование
При каждом удлинении кодов в одной части коды удлиняются нулями, а в другой - единицами. Таким образом, коды одной части не могут быть префиксами другой. Удлинение кода заканчивается тогда и только тогда, когда длина части равна 1, то есть остается единственный код. Таким образом, схема по построению префиксная, а потому разделимая.
Пример
Коды, построенные алгоритмом Фано для заданного распределения вероятностей (n = 7).
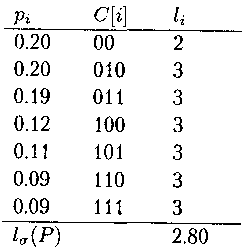
[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
[3]
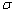 = <аi
= <аi 
 i>ni=1, то любая
схема
i>ni=1, то любая
схема 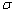 ' = <аi
' = <аi 
 'i>ni=1, где <
'i>ni=1, где < '1, ...,
'1, ...,  'n> является перестановкой <
'n> является перестановкой < 1, ...,
1, ...,  n>. также будет разделимой. Если длины элементарных кодов равны,
то перестановка элементарных кодов в схеме не влияет на длину кода сообщения.
Но если длины элементарных кодов различны, то длина кода сообщения зависит от
состава букв в сообщении и от того, какие элементарные коды каким буквам
назначены.
n>. также будет разделимой. Если длины элементарных кодов равны,
то перестановка элементарных кодов в схеме не влияет на длину кода сообщения.
Но если длины элементарных кодов различны, то длина кода сообщения зависит от
состава букв в сообщении и от того, какие элементарные коды каким буквам
назначены. 1, ...,
1, ...,
 n, соответственно. Тогда, если
ki <= kj и l1 >=
lj, то kili +
kjlj <= kilj +
kjli.
n, соответственно. Тогда, если
ki <= kj и l1 >=
lj, то kili +
kjlj <= kilj +
kjli.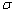 .
.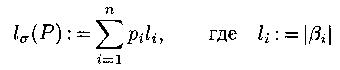
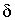 = {а
= {а 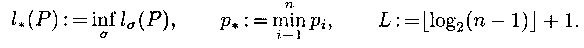
 i |
i |