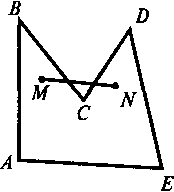
рис.2.1
[Список тем] [Вступление к этой теме] страницы темы: [1] [2] [3] [4] [5]
В школьном курсе математики выпуклыми назывались многоугольники, целиком расположенные по одну сторону от прямых, на которых лежат их стороны.
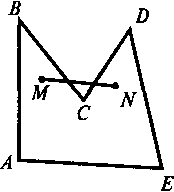
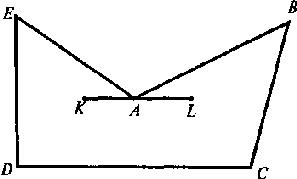
Например, многоугольник на рис. не является выпуклым (он расположен по обе
стороны от прямой ВС).
Общим определяющим свойством, которое отличает выпуклый многоугольник от
невыпуклого, является то, что если взять любые две его точки и соединить их
отрезком, то весь отрезок будет принадлежать этому многоугольнику.
Это свойство может быть принято за определение выпуклого множества точек.
| Определение |
|---|
|
Множество точек называется выпуклым, если оно вместе с любыми
двумя своими точками содержит весь отрезок, соединяющий эти точки. |
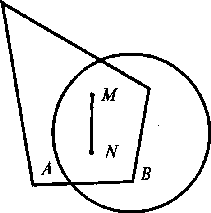
Согласно этому определению многоугольник на рис. а является выпуклым множеством, а многоугольник на рис. 2.1 таковым не является, ибо отрезок MN между двумя его точками М и N не полностью принадлежит этому многоугольнику.
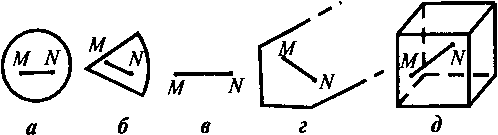
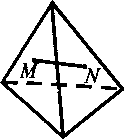
Выпуклыми множествами могут быть не только многоугольники. Примерами выпуклых
множеств являются круг, сектор, отрезок, многоугольная область, куб, пирамида
(рис. 2.2, а-е), многогранная область, прямая, полуплоскость,
полупространство и т.п.
Выпуклые множества обладают важным свойством, которое устанавливается
следующей теоремой.
| Теорема |
|---|
| Пересечение (общая часть) любого числа выпуклых множеств есть выпуклое множество. |
Пусть М и N - любые две точки пересечения двух множеств
А и В (рис. 2.3). Так как точки М и N принадлежат
пересечению множеств, т.е. одновременно и выпуклому множеству А, и
выпуклому множеству В, то согласно определению выпуклого множества
все точки отрезка MN будут принадлежать как множеству А, так
и множеству В, т.е. пересечению этих множеств. А это и означает, что
пересечение данных множеств есть выпуклое множество.
Среди точек выпуклого множества можно выделить внутренние, граничные и угловые
точки.
| Определение |
|---|
| Точка множества называется внутренней, если в некоторой ее окрестности содержатся точки только данного множества. |
|
Точка множества называется граничной, если в любой ее окрестности
содержатся как точки, принадлежащие данному множеству, так и точки, не
принадлежащие ему. |
| Точка множества называется угловой (или крайней), если она не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству. |
| Определение |
|---|
|
Множество точек называется замкнутым, если включает все свои
граничные точки. Множество точек называется ограниченным, если
существует шар (круг) радиуса конечной длины с центром в любой точке множества,
который полностью содержит в себе данное множество; в противном случае множество называется неограниченным. |
Если фигура ограничена только прямыми или их отрезками, то число ее
угловых точек конечно; в случае криволинейности границ фигура содержит
бесконечно много угловых точек, что позволяет сделать следующее определение.
| Определение |
|---|
| Выпуклое замкнутое множество точек пространства (плоскости), имеющее конечное число угловых точек, называется выпуклым многогранником (многоугольником), если оно ограниченное, и выпуклой многогранной (многоугольной) областью, если оно неограниченное. |
До сих пор рассматривались выпуклые множества точек на плоскости и в
пространстве. Аналитически такие точки изображаются упорядоченной парой чисел
(х1, х2) или упорядоченной тройкой чисел
(х1, х2, х3). Понятие точки
можно обобщить, подразумевая под точкой (или вектором) упорядоченный набор
n чисел Х= (х1, х2,: хn),
в котором числа х1, х2,: хn
называются координатами точки (вектора). Такое обобщение имеет смысл, так как
если взять какой-либо экономический объект, то для его характеристики
двух-трех чисел обычно бывает недостаточно и необходимо взять n чисел, где
n > 3.
| Множество всех точек Х= (х1, х2,: хn) образует n-мерное точечное (векторное) пространство. |
При n > 3 точки и фигуры n-мерного пространства не имеют реального геометрического смысла и все исследования объектов этого пространства необходимо проводить в аналитической форме. Тем не менее оказывается целесообразным и в этом случае использовать геометрические понятия для облегчения представлений об объектах n-мерного пространства.
[Список тем] [Вступление к этой теме] страницы темы: [1] [2] [3] [4] [5] [В начало страницы]