 " (p = a
" (p = a  b), это высказывание которое истинно тогда и
только тогда, когда хотя бы одно из первоначальных высказываний истинно.
b), это высказывание которое истинно тогда и
только тогда, когда хотя бы одно из первоначальных высказываний истинно.[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]
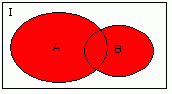
ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (ДИЗЪЮНКЦИЯ) - логическое ИЛИ обозначается в
логических выражениях - "
 " (p = a
" (p = a  b), это высказывание которое истинно тогда и
только тогда, когда хотя бы одно из первоначальных высказываний истинно.
b), это высказывание которое истинно тогда и
только тогда, когда хотя бы одно из первоначальных высказываний истинно.
| Читается: a или b |
Таблица истинности:
|
|
ЛОГИЧЕСКОЕ УМНОЖЕНИЕ (КОНЪЮКЦИЯ) - логическое И, обозначается в логических
выражениях значком -"&" (p = a & b), это высказывание
которое истинно тогда и только тогда когда а и b истинны оба.
| Читается: a и b |
Таблица истинности:
|

|
ОТРИЦАНИЕ (ИНВЕРСИЯ)
обозначается в логических операциях символом " "
перед, или горизонтальной чертой над символом инвертируемого логического
выражения. a или
"
перед, или горизонтальной чертой над символом инвертируемого логического
выражения. a или  a.
читается: не a, или отрицание a.
a.
читается: не a, или отрицание a.
Таблица истинности:
|

|
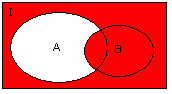
ИМПЛИКАЦИЯ (СЛЕДСТВИЕ)
обозначается в логических операциях стрелкой
"  " от посылки импликации " а " к
ее заключению "b". Это высказывание, которое ложно тогда и только
тогда, когда "а" - истинно, а " b " - ложно.
" от посылки импликации " а " к
ее заключению "b". Это высказывание, которое ложно тогда и только
тогда, когда "а" - истинно, а " b " - ложно.
a  b читается: b читается: |
Таблица истинности: |
||||||||||||||||
|
|
|
ЭКВИВАЛЕНТНОСТЬ
обозначается в логических операциях
 или
или  .
Это высказывание
истинное тогда и только тогда, когда а и b оба истинны или оба ложны.
.
Это высказывание
истинное тогда и только тогда, когда а и b оба истинны или оба ложны.
a  b читается: b читается:
|
Таблица истинности:
|

|
АЛЬТЕРНАТИВНАЯ (ИСКЛЮЧАЮЩАЯ) ДИЗЪЮНКЦИЯ (исключающее ИЛИ)
обозначается в логических операциях знаком кольцевой суммы "
 " Это высказывание - истинное, когда
истинно любое из а или b, но не оба одновременно.
" Это высказывание - истинное, когда
истинно любое из а или b, но не оба одновременно.
а  b читается: b читается:
|
Таблица истинности:
|

|
ЛОГИЧЕСКОЕ И-НЕ (Штрих Шеффера, отрицание конъюнкции)
обозначается в логических операциях значком " | ": a|b.
Это высказывание - истинно, когда любая из посылок (или обе вместе) -
ложны.
|
a|b читается: а и b несовместны. |
Таблица истинности:
|

|
ЛОГИЧЕСКОЕ ИЛИ-НЕ (стрелка Пирса, функция Вебба, отрицание дизъюнкции)
обозначается в логических операциях значком "
 ":
a
":
a b.
b.
Это высказывание - истинно, когда обе посылки ложны.
a b читается: ни а, ни b b читается: ни а, ни b
|
Таблица истинности:
|

|
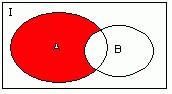
ЗАПРЕТ (отрицание импликации)
обозначается в логических операциях значком "
 ":
a
":
a b.
b.
Это высказывание истинное тогда и только тогда, когда, а истинно при ложном b.
a  b читается: a, но не b; b читается: a, но не b;a, запрет по b. |
|
|
 ).
).
 ).
).
 ).
).
Отличный от этого порядок определяется скобками.
Было доказано (Шеннон, Шестаков, Нейман), что все электронные схемы ЭВМ
могут быть реализованы с помощью логических элементов И, ИЛИ, НЕ.
C помощью основных логических операций (&, ,
,
 ) можно получать из простых высказываний
сложные, затем, объединяя их во все более сложные, получить формулы,
отражающие алгоритмы решения задач любой сложности.
) можно получать из простых высказываний
сложные, затем, объединяя их во все более сложные, получить формулы,
отражающие алгоритмы решения задач любой сложности.
Кроме этого в логике первого порядка используют два специальных
символа чтобы характеризовать переменные. Это символы, называемые
кванторами
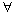 х - читается "для всех х", "для любгого х"
х - читается "для всех х", "для любгого х" х - читается "существует х"
х - читается "существует х"[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]