Р°( ·), Q°( ·,·,...,·) - символы постоянных предикатов.
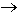 ,
,  .
.
 x,
x,  х.
х.
[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]
В логике предикатов будем пользоваться следующей символикой:
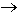 ,
,  .
.
 x,
x,  х.
х.
Определение формулы логики предикатов.
 В , А &
В, А
В , А &
В, А 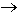 В есть формулы. В этих формулах те переменные,
которые в исходных формулах были свободными, являются свободными, а те,
которые были связанными, являются связанными.
В есть формулы. В этих формулах те переменные,
которые в исходных формулах были свободными, являются свободными, а те,
которые были связанными, являются связанными.
 хА(х) и
хА(х) и
 хА(х) являются формулами, причем предметная
переменная входит в них связанно.
хА(х) являются формулами, причем предметная
переменная входит в них связанно.
Например, если P(x) и Q(x,y) - одноместный и двухместный
предикаты, а q, r - переменные высказывания, то формулами будут слова:
q, P(х) , P(x)&Q(x°,y),  xP(x)
xP(x)
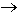
 xQ(x,у), (Q(x,у)
xQ(x,у), (Q(x,у)  q)
q) 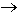 r .
r .
Не является формулой слово:  xQ(x,y)
xQ(x,y)
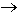 P(x) . Здесь нарушено условие п.З, так как в формулу
P(x) . Здесь нарушено условие п.З, так как в формулу
 xQ(x,y) переменная x входит связано,
а в формулу P(х) переменная x входит свободно.
xQ(x,y) переменная x входит связано,
а в формулу P(х) переменная x входит свободно.
Из определения формулы логики предикатов ясно, что всякая формула алгебры
высказываний является формулой логики предикатов.
О логическом значении формулы логики предикатов можно говорить лишь тогда, когда задано множество М, на котором определены входящие в эту формулу предикаты. Логическое значение формулы логики предикатов зависит от значений трех видов переменных:
При конкретных значениях каждого из трех видов переменных формула логики предикатов становится высказыванием, имеющим истинное или ложное значение.
В качестве примера рассмотрим формулу:
 y
y z(P(x,y)
z(P(x,y)
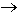 P(y,z)). (1)
P(y,z)). (1)
в которой двухместный предикат Р(х,у) определен на множестве МхМ, где М = {0,1,2,...,n,...} .
В формулу (1) входит переменный предикат Р(х,у), предметные
переменные х, у, z, две из которых у и z — связанные
кванторами, а x - свободная.
Возьмем за конкретное значение предиката Р(х,у) фиксированный предикат
Р°(х,у): “ х < у ”, а свободной переменной x придадим значение
х° = 5  М . Тогда при значениях
у, меньших х° = 5 предикат P0(x0,y)
принимает значение ложь, а импликация P(x, y)
М . Тогда при значениях
у, меньших х° = 5 предикат P0(x0,y)
принимает значение ложь, а импликация P(x, y) 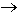 Р(у, z)
при всех z
Р(у, z)
при всех z  М принимают значение истина,
то есть высказывание
М принимают значение истина,
то есть высказывание  y
y  z(P°(x,y)
z(P°(x,y) 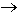 Р0(у,z))
имеет значение ″истина″.
Р0(у,z))
имеет значение ″истина″.
[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]