[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]

Потоки в сетях.

Свободные деревья

Рассмотрим некоторые примеры практических задач.
Пример
1. Пусть имеется сеть автомобильных дорог, по которым можно проехать из пункта А в пункт В. Дороги могут пересекаться в промежуточных пунктах. Количество автомобилей, которые могут проехать по каждому отрезку дороги в единицу времени, не безгранично, оно определяется такими факторами, как ширина проезжей части, качество дорожного покрытия, действующие ограничения скорости движения и т. д. (обычно это называют "пропускной способностью" дороги). Каково максимальное количество автомобилей, которые могут проехать из пункта А в пункт В без образования пробок на дорогах (обычно это называют "автомобильным потоком")? Или же можно поставить другой вопрос: какие дороги и насколько нужно расширить или улучшить, чтобы увеличить максимальный автомобильный поток на заданную величину?
2. Пусть имеется сеть трубопроводов, соединяющих пункт А (скажем, нефтепромысел) с пунктом В (скажем, нефтеперерабатывающим заводом). Трубопроводы могут соединяться и разветвляться в промежуточных пунктах. Количество нефти, которое может быть перекачено по каждому отрезку трубопровода в единицу времени, также не безгранично и определяется такими факторами, как диаметр трубы, мощность нагнетающего насоса и т. д. (обычно это называют "пропускной способностью" или "максимальным расходом" трубопровода). Сколько нефти можно прокачать через такую сеть в единицу времени?
3. Пусть имеется система машин для производства готовых изделий из сырья, и последовательность технологических операций может быть различной (то есть операции могут выполняться на разном оборудовании или в разной последовательности), но все допустимые варианты заранее строго определены. Максимальная производительность каждой единицы оборудования, естественно, также заранее известна и постоянна. Какова максимально возможная производительность всей системы в целом и как нужно организовать производство для достижения максимальной производительности?
Изучение этих и многочисленных подобных им практических задач приводит к теории потоков в сетях. В данном разделе рассматривается решение только одной (но самой существенной) задачи этой теории, а именно задачи определения максимального потока.

1. Определение потока

Пусть G(V, Е) - сеть, s и t - соответственно источник и сток сети. Дуги сети нагружены неотрицательными вещественными числами, с: Е R⁺.

Определение

Если u и v - вершины, то число с(u, v) - называется пропускной способностью дуги (u, v).

Замечание

Матрица пропускных способностей С : array [1..p, 1..p] of real является представлением сети, аналогичным матрице смежности. Элемент С[u, v] = 0 соответствует дуге с нулевой пропускной способностью, то есть отсутствию дуги, а элемент С[u, v] > 0 соответствует дуге с ненулевой пропускной способностью, то есть дуга присутствует.

Пусть задана функция f: Е R.

Определение

Дивергенцией функции f в вершине v называется число div(f, v), которое определяется следующим образом: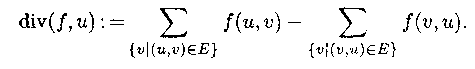

Замечание

В физике дивергенция обычно определяется наоборот: то, что пришло, минус то, что ушло. Но в данном случае удобнее, чтобы дивергенция источника была положительна.

Определение

Функция f: Е К называется потоком в сети G, если: 1. (u, v) Е 0 <= f(u, v) <= c(u, v), то есть поток через дугу неотрицателен и не превосходит пропускной способности дуги; 2. u V \ {s, t} div(f, u) = 0, то есть дивергенция потока равна нулю во всех вершинах, кроме источника и стока. Число w(f): = div(f, s) называется величиной потока f.

2. Разрезы

Пусть Р - (s, t) - paзpeз, Р 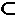Е. Всякий разрез определяется разбиением множества вершин V на два подмножества S Т, так что S V, Т V, S Т = V, S & T = , s S, t T, a в P попадают все дуги, соединяющие S и Т. Тогда Р = P⁺ P^-, где Р⁺ - дуги от S к Т, Р^- - дуги от Т к S. Сумма потоков через дуги разреза Р обозначается F(P). Сумма пропускных способностей дуг разреза Р называется пропускной способностью разреза и обозначается С(Р):

3. Теорема Форда и Фалкерсона

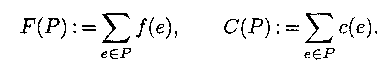
ЛЕММА

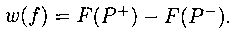
доказательство
Рассмотрим сумму

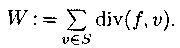
Пусть дуга (u. v) Е. Если u, v S, то в сумму W попадают два слагаемых для этой дуги: +f(u, v) при вычислении div(f, u) и -f(u, v) при вычислении div(f, u), итого 0. Если u S, v T, то в сумму W попадает одно слагаемое +f(u, v), все такие слагаемые дают F(P⁺). Если u Т, v S, то в сумму W попадает одно слагаемое -f(u, v), все такие слагаемые дают F(P^-). Таким образом, W = F(P⁺) - F(P^-). С другой стороны,

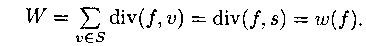
ЛЕММА

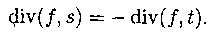
доказательство
Рассмотрим разрез Р: = (S, T), где S: = V \ {t}, а T: = {t}. Имеем:

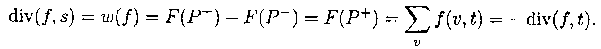
ЛЕММА

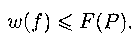
доказательство

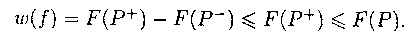
ЛЕММА


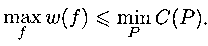
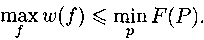
доказательство
По предыдущей лемме w(f) <= F(P), следовательно,

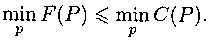
По определению F(P) <= С(Р), следовательно,
Имеем:

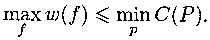
ТЕОРЕМА (Форда и Фалкерсона)

Максимальный поток в сети равен минимальной пропускной способности разреза, то есть существует поток f*, такой что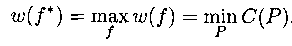

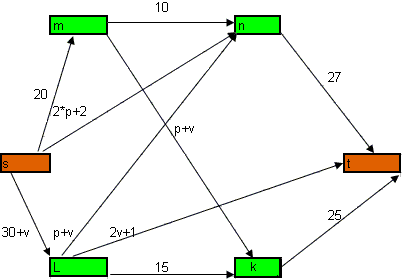
Доказательство
Пусть f - некоторый максимальный поток. Покажем, что существует разрез Р, такой что w(f) = С(Р). Рассмотрим граф G', полученный из сети G отменой ориентации ребер. Построим множество вершин S следующим образом:

то есть вдоль пути <s, u> дуги в направлении пути не насыщены, а дуги против направления пути имеют положительный поток. Такая цепь <s, u> называется аугменталъной. Имеем s S по построению. Следовательно, S . Положим Т: = V \ S. Покажем, что t T. Действительно, пусть t S. Тогда существует аугментальная цепь <s, t>, обозначим ее R. Но тогда можно найти число d:

В этом случае можно увеличить величину потока на S, изменив поток для всех дуг аргументальной цепи:

При этом условия потока выполняются: 0 <= f(е) <= С(е), div(v) = 0.
Таким образом, ноток f увеличен на величину d , что противоречит максимальности потока f. Имеем t Т и T . Следовательно, S и T определяют разрез Р = Р⁺ Р^-. В этом разрезе все дуги е⁺ насыщены (f(е⁴) = С(е⁺)), а все дуги е^- не нагружены (f(е^-) = 0), иначе S можно было бы расширить. Имеем: w(f) = F(P⁺) - F(P^-) = C(P⁺), таким образом, Р+ - искомый разрез.

4. Алгоритм нахождения максимального потока

Следующий алгоритм определяет максимальный поток в сети, заданной матрицей пропускных способностей дуг. Этот алгоритм использует ту же идею доказательства теоремы Форда и Фалкерсона, а именно, задавшись начальным приближением потока, определяется множество вершин S, которые соединены аргументальными цепями с источником s. Если оказывается, что t S, то это означает, что поток не максимальный и его можно увеличить на величину d. Для определения аргументальных цепей и одновременного подсчета величины d в алгоритме использована вспомогательная структура данных:

Р : array [1..p] of record s : enum (-, +) { "знак", то есть направление дуги } n : 1..р { предшествующая вершина в аргументальной цепи } S : real { величина возможного увеличения потока } end record

Алгоритм 1. Нахождение максимального потока

Вход: сеть G(V, Е) с источником s и стоком t, заданная матрица пропускных способностей С : array [1..p, 1..p] of real. Выход: матрица максимального потока F : array [1..p, 1..p] of real. for u, v V do F[u, v]: = 0{ вначале поток нулевой } end for M : { итерация увеличения потока } for v V do S[v]: = 0; N[v]: = 0; P[v]:= (,,) { инициализация } end for S[s]: = 1; P[s]: = (+, s, ){ так как s S } repeat a: = 0{ признак расширения S } for v V do if S[v] = 1 & N[v] = 0 then for u Г(v) do if S[u] = 0&F[v, u] < C[v, u] then S[u]: = 1; P[u]:= (+, v, min(P[v].d, C[v, u] - F[v, u])); a: = 1 end if end for for u F-1(v) do if S[u] = 0&F[u, v] >0 then S[u]: = 1; P[u]: = (-, v, min[P[v].d, F[u, v])); a: = 1 end if end for N[v]: = 1 end if end for if S[t] then x:= t; d:= P[t].d while x s do if P[a].s = + then F[P[x].n, x]: = F[P[x].n, x] + S else F[x, P[x].n]:= F[x, P[x].n]- d end if x: = P[x].n end while goto M end if until a = 0

обоснование
В качестве первого приближения берется нулевой поток, который по определению является допустимым. В основном цикле, помеченном меткой M, делается попытка увеличить поток. Для этого в цикле repeat расширяется, пока это возможно, множество S вершин, достижимых из вершины s по аргументальным цепям. При этом, если в множество S попадает вершина t, то поток вдоль найденной аргументальной цепи <s, t> немедленно увеличивается на величину d, и начинается новая итерация с целью увеличить поток. Процесс расширения множества S в цикле repeat заканчивается, потому что множество вершин конечно, а отмеченные в массиве N вершины повторно не рассматриваются. Если процесс расширения множества S заканчивается и при этом вершина t не попадает в множество S, то по теореме Форда и Фалкерсона найденный поток F является максимальным и работа алгоритма завершается.

ЗАМЕЧАНИЕ

Приведенный алгоритм не является самым эффективным.

5. Связь между теоремой Менгера и теоремой Форда и Фалкерсона

Теорема Менгера является фундаментальным результатом, который проявляется в различных формах. Теорема Форда и Фалкерсона также может быть получена из теоремы Менгера. Далее приведена схема неконструктивного доказательства теоремы Форда и Фалкерсона на основе теоремы Менгера. Сначала нужно получить вариант теоремы Менгера в ориентированной реберной форме: наибольшее число <s, t>-путей, непересекающихся по дугам, равно наименьшему числу дуг в (s, t)-разрезе. Это теорема Форда и Фалкерсона в том случае, когда e Е С(е) = 1. Действительно, пусть Q - множество дуг из максимального набора непересекающихся <s, t>-путей. Назначим f(е): = 1, если е Q, и f(е): = 0, если е Q. Это поток, так как дивергенция в любой вершине равна 0 и поток через дугу не превосходит пропускной способности. Величина этого потока равна k <= d⁺(s), где k - число дуг, выходящих из s, которые начинают пути из Q. Этот поток максимальный. Действительно, если положить f(е): = а > 0 для е Q, то

1. если дуга е входит в вершину, входящую в пути из Q, или выходит из такой вершины, то нарушается условие потока (дивергенция -а или +а, соответственно);
2. если вновь назначенные дуги с ненулевыми потоками образуют новый <s, t>-путь, то это противоречит выбору Q.

Пусть теперь пропускные способности суть натуральные числа. Тогда можно провести аналогичные рассуждения для мультиграфов, считая, что вместо одной дуги с пропускной способностью n имеется n дуг с пропускной способностью 1. Если пропускные способности - рациональные числа, то их можно привести к общему знаменателю и свести задачу к предыдущему случаю.
Для вещественных пропускных способностей заключение теоремы можно получить путем перехода к пределу в условиях предыдущего случая.

ОТСТУПЛЕНИЕ

Приведенное в подразделе 3 доказательство теоремы Форда и Фалкерсона конструктивно, из него не только следует заключение о величине максимального потока, но и извлекается способ нахождения максимального потока.

Упражнения

[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]