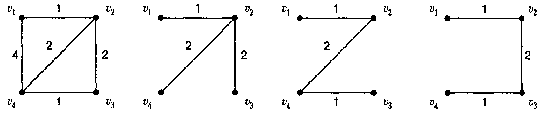
Рис. 14. Граф, дерево кратчайших путей и два кратчайших остова
[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]
Кратчайший остов Задача отыскания кратчайшего остова графа является классической задачей теории графов. Методы решения этой задачи послужили основой для многих других важных результатов. В частности, исследования алгоритма Краскала, описанного в подразделе 3, привели в конечном счете к теории жадных алгоритмов.
Определение | Пусть G(V, E) - граф. Остовной подграф графа G(V, Е) - это подграф, содержащий все вершины. Остовный подграф, являющийся деревом, называется остовом. |
ЗАМЕЧАНИЕ |
Остов определяется множеством ребер, поскольку вершины остова суть
вершины графа. Несвязный граф не имеет остова. Связный граф может иметь много остовов. |
ОТСТУПЛЕНИЕ | Если задать длины ребер, то можно поставить задачу нахождения кратчайшего остова. Эта задача имеет множество практических интерпретаций. Например, пусть задано множество аэродромов и нужно определить минимальный (по сумме расстояний) набор авиарейсов, который позволил бы перелететь с любого аэродрома на любой другой. Решением этой задачи будет кратчайший остов полного графа расстояний между аэродромами. |
ЗАМЕЧАНИЕ | Существует множество различных способов найти какой-то остов графа. Например, алгоритм поиска в глубину строит остов (по ребрам возврата). Множество кратчайших путей из заданной вершины ко всем остальным также образует остов. Однако этот остов может не быть кратчайшим. |
Рассмотрим следующую схему алгоритма построения кратчайшего остова.
Пусть Т - множество непересекающихся деревьев, являющихся подграфами
графа G. Вначале T состоит из отдельных вершин графа G,
в конце Т содержит единственный элемент - кратчайший остов графа
G.
Построение кратчайшего остова |
Вход: граф G(V, Е), заданный матрицей длин ребер С. Выход: кратчайший остов Т. T:=V while в T больше одного элемента do взять любое поддерево из T найти к нему ближайшее соединить эти деревья в T end while |
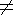 0. Положим
0. Положим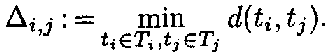
 i,j всегда реализуется на некотором ребре
с длиной сi,j. Далее индукцией по шагам алгоритма покажем,
что все ребра, включенные в Т, принадлежат кратчайшему остову - SST.
Вначале выбранных ребер нет, поэтому их множество включается в кратчайший
остов. Пусть теперь все ребра, добавленные в T, принадлежат SST.
Рассмотрим очередной шаг алгоритма. Пусть на этом шаге добавлено ребро
(i, j), соединяющее поддерево Ti с поддеревом
Tj. Если (i, j)
i,j всегда реализуется на некотором ребре
с длиной сi,j. Далее индукцией по шагам алгоритма покажем,
что все ребра, включенные в Т, принадлежат кратчайшему остову - SST.
Вначале выбранных ребер нет, поэтому их множество включается в кратчайший
остов. Пусть теперь все ребра, добавленные в T, принадлежат SST.
Рассмотрим очередной шаг алгоритма. Пусть на этом шаге добавлено ребро
(i, j), соединяющее поддерево Ti с поддеревом
Tj. Если (i, j) 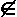 SST, то,
поскольку SST является деревом и, стало быть, связен,
SST, то,
поскольку SST является деревом и, стало быть, связен, 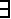 (i*, j*)
(i*, j*) 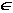 SST, соединяющее
Ti с остальной частью SST. Тогда удалим из SST ребро
(i*, j*) и добавим ребро (i, j): SST': = SST-
(i*, j*) + (i, j). Полученный подграф SST' является остовом, причем
более коротким, чем SST, что противоречит выбору SST
(SST - Shortest Sceleton Tree - стандартное обозначение для
кратчайшего остова).
SST, соединяющее
Ti с остальной частью SST. Тогда удалим из SST ребро
(i*, j*) и добавим ребро (i, j): SST': = SST-
(i*, j*) + (i, j). Полученный подграф SST' является остовом, причем
более коротким, чем SST, что противоречит выбору SST
(SST - Shortest Sceleton Tree - стандартное обозначение для
кратчайшего остова).ЗАМЕЧАНИЕ | Различные способы выбора поддерева для наращивания на первом шаге тела цикла дают различные конкретные варианты алгоритма построения SST. |
Следующий жадный алгоритм, известный как алгоритм Краскала, находит
кратчайший остов в связном графе.
Алгоритм Краскала |
Вход: список Е ребер графа G с длинами. Выход: множество Т ребер кратчайшего остова. Т:= 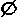 упорядочить Е в порядке возрастания длин k: = 1 { номер рассматриваемого ребра } for i from 1 to p - 1 do while добавление ребра E(k) образует цикл в T do k: = k + 1 { пропустить это ребро } end while T: = T 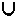 {E[k]}
{ добавить это ребро в SST } {E[k]}
{ добавить это ребро в SST }end for |
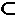 Е - произвольное множество ребер, a G' -
правильный подграф графа G, определяемый этими ребрами. Очевидно, что
любое максимальное не содержащее циклов подмножество множества Е'
является объединением остовов компонент связности G' и по теореме об
основных свойствах деревьев содержит p(G') - k(G') элементов. Таким
образом, множество ациклических подмножеств ребер образует матроид. Далее,
рассматриваемый алгоритм, как жадный алгоритм, находит кратчайшее ациклическое
подмножество множества ребер. По построению оно содержит р - 1 элемент,
а значит, является искомым остовом.
Е - произвольное множество ребер, a G' -
правильный подграф графа G, определяемый этими ребрами. Очевидно, что
любое максимальное не содержащее циклов подмножество множества Е'
является объединением остовов компонент связности G' и по теореме об
основных свойствах деревьев содержит p(G') - k(G') элементов. Таким
образом, множество ациклических подмножеств ребер образует матроид. Далее,
рассматриваемый алгоритм, как жадный алгоритм, находит кратчайшее ациклическое
подмножество множества ребер. По построению оно содержит р - 1 элемент,
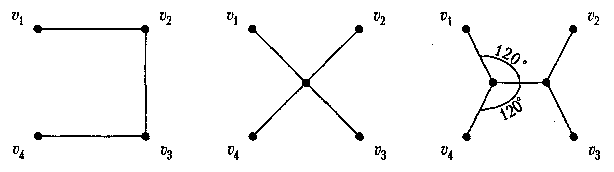
а значит, является искомым остовом.ОТСТУПЛЕНИЕ | Задача о нахождении кратчайшего остова принадлежит к числу немногих задач теории графов, которые можно считать полностью решенными. Между тем, если изменить условия задачи, на первый взгляд даже незначительно, то она оказывается значительно более трудной. Рассмотрим следующую задачу. Пусть задано множество городов на плоскости и нужно определить минимальный (по сумме расстояний) набор железнодорожных линий, который позволил бы переехать из любого города в любой другой. Кратчайший остов полного графа расстояний между городами не будет являться решением этой (практически, очевидно, очень важной) задачи, известной как задача Штейнера. На рис. 15 приведены, соответственно, диаграммы кратчайшего остова, наивного "решения" задачи Штейнера и правильного решения для случая, когда города расположены в вершинах квадрата. |
Комментарии
Материал этой главы затрагивает вопросы, которые очень часто возникают в практическом программировании. Поэтому различные сведения о деревьях можно найти не только в специальных учебниках по теории графов, но и в книгах по программированию и конструированию эффективных алгоритмов.
1. Нарисовать диаграммы всех деревьев с 5 вершинами.
2. Допустим, что в ордереве все узлы, кроме листьев, имеют одну и ту же полустепень исхода n. В этом случае говорят, что дерево имеет постоянную ширину ветвления n. Оценить высоту h ордерева, которое имеет р узлов и постоянную ширину ветвления n.
[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]