[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]

Задача кодирования

Вопросы кодирования издавна играли заметную роль в математике.

Определение
Кодирование - это представление одних объектов при помощи других.

Пример

1. Десятичная позиционная система счисления — это способ кодирования натуральных чисел. Римские цифры — другой способ кодирования натуральных чисел, причем гораздо более наглядный и естественный: палец — I, пятерня — V, две пятерни — X. Однако при этом способе кодирования труднее выполнять арифметические операции над большими числами, поэтому он был вытеснен позиционной десятичной системой.
2. Декартовы координаты — способ кодирования геометрических объектов числами.

Ранее средства кодирования играли вспомогательную роль и не рассматривались как отдельный предмет математического изучения, но с появлением компьютеров ситуация радикально изменилась. Кодирование буквально пронизывает информационные технологии и является центральным вопросом при решении самых разных (практически всех) задач программирования:

• представление данных произвольной природы (например чисел, текста, графики) в памяти компьютера;
• защита информации от несанкционированного доступа;
• обеспечение помехоустойчивости при передаче данных по каналам связи;
• сжатие информации в базах данных.

Само составление текста программы часто и совершенно справедливо называют кодированием.

Не ограничивая общности, задачу кодирования можно сформулировать следующим образом.
Пусть заданы алфавиты А = {a₁, ..., a_n}, В = {b₁, ..., b_m} и функция F: S В*, где S — некоторое множество слов в алфавите А, S А*. Тогда

Определение
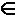функция F называется кодированием, A - первичным алфавитом, B - вторичным, элементы множества S — сообщениями, а элементы = F( α ), α S, 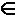B* — кодами (соответствующих сообщений). Обратная функция F-1 (если она существует!) называется декодированием.

Если |В| = m, то F называется m-ичным кодированием. Наиболее распространенный случай В = {0, 1} — двоичное кодирование. Именно этот случай рассматривается в последующих разделах; слово “двоичное” опускается.
Типичная задача теории кодирования формулируется следующим образом: при заданных алфавитах А, В и множестве сообщений S найти такое кодирование F, которое обладает определенными свойствами (то есть удовлетворяет заданным ограничениям) и оптимально в некотором смысле. Критерий оптимальности, как правило, связан с минимизацией длин кодов. Свойства, которые требуются от кодирования, бывают самой разнообразной природы:

• существование декодирования — это очень естественное свойство, однако даже оно требуется не всегда. Например, трансляция программы на языке высокого уровня в машинные команды — это кодирование, для которого не требуется однозначного декодирования;
• помехоустойчивость, или исправление ошибок: функция декодирования F^-1 обладает таким свойством, что F^-1( ) = F^-1( '), если ' в определенном смысле близко к ;
• заданная сложность (или простота) кодирования и декодирования. Например, в криптографии изучаются такие способы кодирования, при которых имеется просто вычисляемая функция F, но определение функции F^-1 требует очень сложных вычислений.

Большое значение для задач кодирования имеет природа множества сообщений S. При одних и тех же алфавитах А, В и требуемых свойствах кодирования F оптимальные решения могут кардинально отличаться для разных S. Для описания множества S (как правило, очень большого или бесконечного) применяются различные методы:

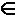• теоретико-множественное описание, например S = {α | α А* & |α| = n};

• вероятностное описание, например S = А*, и заданы вероятности р_i появления букв в сообщении, ⁿ_i=1р_i = 1;

• логико-комбинаторное описание, например, S задано порождающей формальной грамматикой.

[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3]