[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
Сжатие данных
При кодировании наблюдается некоторый баланс между временем и памятью.
Затрачивая дополнительные усилия при кодировании и декодировании, можно
сэкономить память, и, наоборот, пренебрегая оптимальным использованием памяти,
можно существенно выиграть во времени кодирования и декодирования. Конечно,
этот баланс имеет место только в определенных пределах, и нельзя сократить
расход памяти до нуля или построить мгновенно работающие алгоритмы кодирования. Для алфавитного кодирования пределы возможного установлены ранее. Для достижения дальнейшего прогресса нужно рассмотреть неалфавитное кодирование.
1. Сжатие текстов
Допустим, что имеется некоторое сообщение, которое закодировано каким-то
общепринятым способом (для текстов это, например, код ASCII) и хранится в
памяти компьютера. Заметим, что равномерное кодирование (в частности, ASCII)
не является оптимальным для текстов. Действительно, в текстах обычно
используется существенно меньше, чем 256 символов (в зависимости от языка — примерно 60-80 с учетом знаков препинания, цифр, строчных и прописных букв). Кроме того, вероятности появления букв различны и для каждого естественного языка известны (с некоторой точностью) частоты появления букв в тексте. Таким образом, можно задаться некоторым набором букв и частотами их появления в тексте и с помощью алгоритма Хаффмена построить оптимальное алфавитное кодирование текстов (для заданного алфавита и языка). Простые расчеты показывают, что такое кодирование для распространенных естественных языков будет иметь цену кодирования несколько меньше 6, то есть даст выигрыш по сравнению с кодом ASCII на 25% или несколько больше.
Методы кодирования, которые позволяют построить (без потери информации!) коды
сообщений, имеющие меньшую длину по сравнению с исходным сообщением,
называются методами сжатия (или упаковки) данных. Качество сжатия определяется
коэффицентом сжатия, который обычно измеряется в процентах и показывает, на
сколько процентов кодированное сообщение короче исходного.
Известно, что практические программы сжатия (arj, ziр и другие) имеют гораздо
лучшие показатели: при сжатии текстовых файлов коэффициент сжатия достигает
70% и более. Это означает, что в таких программах используется не алфавитное
кодирование.
2. Предварительное построение словаря
Рассмотрим следующий способ кодирования.
- Исходное сообщение по некоторому алгоритму разбивается на
последовательности символов, называемые словами (слово может иметь одно или
несколько вхождений в исходный текст сообщения).
- Полученное множество слов считается буквами нового алфавита. Для этого
алфавита строится разделимая схема алфавитного кодирования (равномерного
кодирования или оптимального кодирования, если для каждого слова подсчитать
число вхождений в текст). Полученная схема обычно называется словарем, так
как она сопоставляет слову код.
- Далее код сообщения строится как пара — код словаря и последовательность
кодов слов из данного словаря.
- При декодировании исходное сообщение восстанавливается путем замены кодов
слов на слова из словаря.
Пример
Допустим, что требуется кодировать тексты на русском языке. В качестве
алгоритма деления на слова примем естественные правила языка: слова отделяются
друг от друга пробелами или знаками препинания. Можно принять допущение, что в
каждом конкретном тексте имеется не более 216 различных слов (обычно
гораздо меньше). Таким образом, каждому слову можно сопоставить номер — целое
число из двух байтов (равномерное кодирование). Поскольку в среднем слова
русского языка состоят более чем из двух букв, такое кодирование дает
существенное сжатие текста (около 75% для обычных текстов на русском языке).
Если текст достаточно велик (сотни тысяч или миллионы букв), то дополнительные
затраты на хранение словаря оказываются сравнительно небольшими.
| Замечание |
|---|
|
Данный метод попутно позволяет решить задачу полнотекстового поиска, то есть
определить, содержится ли заданное слово (или слова) в данном тексте, причем
для этого не нужно просматривать весь текст (достаточно просмотреть только
словарь).
|
Указанный метод можно усовершенствовать следующим образом. На шаге 2 следует
применить алгоритм Хаффмена для построения оптимального кода, а на шаге 1 —
решить экстремальную задачу разбиения текста на слова таким образом, чтобы
среди всех возможных разбиений выбрать то, которое дает наименьшую цену
кодирования на шаге 2. Такое кодирование будет “абсолютно” оптимальным. К
сожалению, указанная экстремальная задача очень трудоемка, поэтому на практике
не используется — время на предварительную обработку большого текста
оказывается чрезмерно велико.
3. Алгоритм Лемпела—Зива
На практике используется следующая идея, которая известна также как
адаптивное сжатие. За один проход по тексту одновременно динамически строится
словарь и кодируется текст. При этом словарь не хранится — за счет того, что
при декодировании используется тот же самый алгоритм построения словаря,
словарь динамически восстанавливается.
Здесь приведена простейшая реализация этой идеи, известная как алгоритм
Лемпела-Зива. Вначале словарь D : аrrау [int] of
string содержит пустое слово, имеющее код 0. Далее в тексте
последовательно выделяются слова. Выделяемое слово — это максимально длинное
слово из уже имеющихся в словаре плюс еще один символ. В сжатое представление
записывается найденный код слова и расширяющая буква, а словарь пополняется
расширенной комбинацией.
| Алгоритм 3. Упаковка по методу Лемпела-Зива |
|---|
Вход: исходный текст, заданный массивом кодов символов f :
аrrау [1..n] of char.
Выход: сжатый текст, представленный последовательностью пар <p,
q>, где р — номер слова в словаре, q — код дополняющей
буквы.
D[0]: =""; d: = 0 { начальное состояние словаря }
k: = 1 { номер текущей буквы в исходном тексте }
while k <= n do
р: = FD(k) { р — индекс найденного слова в словаре }
l: = Length(D[р]) { l — длина найденного слова в
словаре }
yield <p, f[k + l]> { код найденного слова и еще одна
буква }
d: = d + 1; D[d]: = D[р] 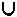 f[k + l]
{ пополнение словаря, здесь f[k + l]
{ пополнение словаря, здесь 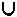 — это конкатенация } — это конкатенация }
k: = k + l + 1 { продвижение вперед по исходному тексту }
end while
|
Слово в словаре ищется с помощью несложной функции FD.
|
Вход: k – номер символа в исходном тексте, начиная с которого
нужно искать в тексте слова из словаря.
Выход: р — индекс самого длинного слова в словаре, совпадающего
с символами
f[k]..f[k + l]. Если такого слова в словаре нет, то р = 0.
l: = 0; р: = 0 { начальное состояние }
for i from 1 to d do
if D[i] = f[k..k + Length(D[i]) – 1] &
length(D[i]) > l then
р: = i; l: = Length(D[i]) { нашли более подходящее
слово }
end if
end for
return p
|
Распаковка осуществляется следующим алгоритмом.
| Алгоритм 4. Распаковка по методу Лемпела-Зива |
|---|
Вход: сжатый текст, представленный массивом пар g : аrrау
[1..m] оf record p : int; q : char
endrecord, где р — номер слова в словаре, q — код дополняющей
буквы.
Выход: исходный текст, заданный последовательностью строк и символов.
D[0]: =""; d: = 0 { начальное состояние словаря }
for k <= n do
р: = g[k].р { р — индекс слова в словаре }
q: = g[k].q { q — дополнительная буква }
yield p 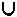 q { вывод слова и еще одной
буквы } q { вывод слова и еще одной
буквы }
d: = d + 1; D[d]: = D[р] 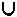 q { пополнение словаря, здесь
q { пополнение словаря, здесь 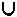 — это конкатенация
} — это конкатенация
}
end for
|
| Замечание |
|---|
На практике применяют различные усовершенствования этой схемы.
- Словарь можно сразу инициализировать, например, кодами символов (то есть
считать, что однобуквенные слова уже известны).
- В текстах часто встречаются регулярные последовательности: пробелы и
табуляции в таблицах и т. п. Сопоставлять каждой подпоследовательности такой
последовательности отдельное слово в словаре нерационально. В таких случаях
лучше применить специальный прием, например, закодировать последовательность
пробелов парой <k, s>, где k — количество пробелов, а
s — код пробела.
|
[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
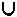 f[k + l]
{ пополнение словаря, здесь
f[k + l]
{ пополнение словаря, здесь 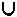 — это конкатенация }
— это конкатенация }