[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
Шифрование
Защита компьютерных данных от несанкционированного доступа, искажения и уничтожения в настоящее время является серьезной социальной проблемой. Применяются различные подходы к решению этой проблемы.
- Поставить между злоумышленником и данными в компьютере непреодолимый
барьер, то есть исключить саму возможность доступа к данным путем физической
изоляции компьютера с данными, применения аппаратных ключей защиты и т. п.
Такой подход надежен, но он затрудняет доступ к данным и легальным
пользователям, а потому постепенно уходит в прошлое.
- Поставить между злоумышленником и данными в компьютере логический барьер,
то есть проверять наличие прав на доступ к данным и блокировать доступ при
отсутствии таких прав. Для этого применяются различные системы паролей,
регистрация и идентификация пользователей, разграничения прав доступа и т. п.
Практика показывает, что борьба между “хакерами” и модулями защиты
операционных систем идет с переменным успехом.
- Хранить данные таким образом, чтобы они могли “сами за себя постоять”.
Другими словами, так закодировать данные, чтобы даже получив их, злоумышленник
не смог бы нанести ущерба.
Этот раздел посвящен обсуждению методов кодирования, применяемых в последнем
случае.
1. Криптография
Шифрование — это кодирование данных с целью защиты от
несанкционированного доступа.
Процесс кодирования сообщения называется шифрованием (или зашифровкой),
а процесс декодирования — расшифровыванием (или расшифровкой).
Само кодированное сообщение называется шифрованным (или просто шифровкой),
а применяемый метод называется шифром.
Основное требование к шифру состоит в том, чтобы расшифровка (и, может быть,
зашифровка) была возможна только при наличии санкции, то есть некоторой
дополнительной информации (или устройства), которая называется ключом шифра.
Процесс декодирования шифровки без ключа называется дешифрованием (или
дешифрацией, или просто раскрытием шифра).
Область знаний о шифрах, методах их создания и раскрытия называется
криптографией (или тайнописью).
Свойство шифра противостоять раскрытию называется криптостойкостью (или
надежностью) и обычно измеряется сложностью алгоритма дешифрации.
| Отступление |
|---|
|
В практической криптографии криптостойкость шифра оценивается из экономических
соображений. Если раскрытие шифра стоит (в денежном выражении, включая
необходимые компьютерные ресурсы, специальные устройства и т. п.) больше, чем
сама зашифрованная информация, то шифр считается достаточно надежным.
|
Криптография известна с глубокой древности и использует самые разнообразные
шифры, как чисто информационные, так и механические. В настоящее время
наибольшее практическое значение имеет защита данных в компьютере, поэтому ]
далее рассматриваются программные шифры для сообщений в алфавите {0, 1}.
2. Шифрование с помощью случайных чисел
Пусть имеется датчик псевдослучайных чисел, работающий по некоторому
определенному алгоритму. Часто используют следующий алгоритм:
Ti+1:= (а * Ti + b) mod c,
где Тi — предыдущее псевдослучайное число,
Ti+1 — следующее псевдослучайное число, а коэффициенты
a, b, с постоянны и хорошо известны. Обычно с = 2n, где n
— разрядность процессора, а mod 4 = 1, а b — нечетное.
В этом случае последовательность псевдослучайных чисел имеет период с.
Процесс шифрования определяется следующим образом. Шифруемое сообщение
представляется в виде последовательности слов S0,
S1, ..., каждое длины n, которые складываются по модулю 2 со
словами последовательности T0, T1, ..., то есть
Ci := Si A Ti.
Последовательность Т0, T1, ... называется гаммой
шифра.
Процесс расшифровывания заключается в том, чтобы еще раз сложить шифрованную
последовательность с той же самой гаммой шифра:
Si := Ci A Ti.
Ключом шифра является начальное значение Т0, которое
является секретным и должно быть известно только отправителю и получателю
шифрованного сообщения.
| Замечание |
|---|
|
Шифры, в которых для зашифровки и расшифровки используется один и тот же ключ,
называются симметричными.
|
Если период последовательности псевдослучайных чисел достаточно велик, чтобы
гамма шифра была длиннее сообщения, то дешифровать сообщение можно только
подбором ключа. При увеличении n экспоненциально увеличивается криптостойкость
шифра.
| Отступление |
|---|
|
Это очень простой, и эффективный метод часто применяют “внутри” программных
систем, например, для защиты данных на локальном диске. Для защиты данных,
передаваемых по открытым каналам связи, особенно в случае многостороннего
обмена сообщениями, этот метод применяют не так часто, поскольку возникают
трудности с надежной передачей секретного ключа многим пользователям.
|
3. Криптостойкость
Описанный в предыдущем подразделе метод шифрования обладает существенным
недостатком. Если известна хотя бы часть исходного сообщения, то все сообщение
может быть легко дешифровано. Действительно, пусть известно одно исходное слово
Si. Тогда
Ti := Ci A Si.
и далее вся правая часть гаммы шифра определяется по указанной формуле датчика
псевдослучайных чисел.
| Замечание |
|---|
|
На практике часть сообщения вполне может быть известна злоумышленнику.
Например, многие текстовые редакторы помещают в начало файла документа одну и
ту же служебную информацию. Если злоумышленнику известно, что исходное
сообщение подготовлено в данном редакторе, то он сможет легко дешифровать
сообщение.
|
Для повышения криптостойкости симметричных шифров применяют различные приемы:
- вычисление гаммы шифра по ключу более сложным (или секретным) способом;
- применение вместо A более сложной (но обратимой) операции для вычисления
шифровки;
- предварительное перемешивание битов исходного сообщения по фиксированному
алгоритму.
Наиболее надежным симметричным шифром считается DES (Data Encryption
Standard), в котором используется сразу несколько методов повышения
криптостойкости.
В настоящее время широкое распространение получили шифры с открытым ключом.
Эти шифры не являются симметричными — для зашифровки и расшифровки
используются разные ключи. При этом ключ, используемый для зашифровки,
является открытым (не секретным) и может быть сообщен всем желающим, отправить
шифрованное сообщение, а ключ, используемый для расшифровки, является закрытым
и хранится в секрете получателем шифрованных сообщений. Даже знание всего
зашифрованного сообщения и открытого ключа, с помощью которого оно было
зашифровано, не позволяет дешифровать сообщение (без знания закрытого ключа).
Для описания метода шифрования с открытым ключом нужны некоторые факты из
теории чисел, изложенные (без доказательств) в следующем подразделе.
4. Модулярная арифметика
В этом подразделе все числа целые. Говорят, что число a сравнимо по
модулю n с числом b (обозначение: а
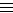 b (mod n)), если а и b при делении на n дают один и
тот же остаток:
b (mod n)), если а и b при делении на n дают один и
тот же остаток:
a 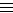 b (mod n): = a mod n = b mod n.
b (mod n): = a mod n = b mod n.
Отношение сравнимости рефлексивно, симметрично и транзитивно и является
отношением эквивалентности. Классы эквивалентности по отношению сравнимости
(по модулю n) называются вычетами (по модулю n). Множество
вычетов по модулю n обозначается Zn. Обычно из
каждого вычета выбирают одного представителя — неотрицательное число, которое
при делении на n дает частное 0. Это позволяет считать, что
Zn = {0, 1, 2, ..., n - 1}, и упростить обозначения.
Над вычетами (по модулю n) определены операции сложения и умножения по
модулю n, обозначаемые, соответственно, +n и
•n и определяемые следующим образом:
a +n b:= (a + b) mod n, a •n b:= (а • b)
mod n.
| Замечание |
|---|
|
Если из контекста ясно, что подразумеваются операции по модулю n, то
индекс n опускается.
|
Легко видеть, что <Zn; +n> образует абелеву
группу, а <Zn; +n, •n>
— коммутативное кольцо с единицей.
Рассмотрим Z*n — подмножество Zn чисел,
взаимно простых с n.
| Замечание |
|---|
|
Числа а и b называются взаимно простыми, если их наибольший общий
делитель равен 1
|
Можно показать, что <Zn; •n> — абелева
группа. Таким образом, для чисел из множества Z*n существуют
обратные по умножению по модулю n.
| Замечание |
|---|
|
Если n — простое число, то <Z*n; +n,
*n> является полем.
|
Функция 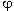 (n): = |Z*n| называется
функцией Эйлера.
(n): = |Z*n| называется
функцией Эйлера.
| Замечание |
|---|
Если р — простое число, то 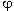 (р) = р - 1,
и вообще, (р) = р - 1,
и вообще, 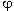 (n) < n. (n) < n. |
Можно показать, что

где p1, ..., pk — все простые делители n.
Имеет место следующая теорема.
| Теорема (Эйлера) |
|---|
Если n > 1, то
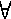 a a 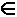 Z*n aφ(n)
Z*n aφ(n) 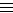 1 (mod n).
1 (mod n).
|
Отсюда непосредственно выводима
| Теорема (малая теорема Ферма) |
|---|
Если р > 1 — простое число, то
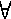 a
a 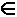 Z*p ap-1
Z*p ap-1 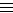 1 (mod p).
1 (mod p).
|
Имеет место, следующее утверждение.
| Теорема |
|---|
Если числа n1, ..., nk попарно взаимно простые, число
n = n1n2 ... nk — их произведение, х и а —
целые числа, то
x 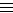 a (mod n) ↔ a (mod n) ↔
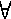 i i 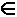 1..k
x 1..k
x 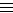 a (mod ni). a (mod ni).
|
| Замечание |
|---|
|
Последнее утверждение является следствием теоремы, которая известна как
″китайская теорема об остатках″.
|
Шифрование с открытым ключом производится следующим образом.
- Получателем сообщений производится генерация открытого ключа (пара чисел
n и е) и закрытого ключа (число d). Для этого:
- выбираются два простых числа р и q;
- определяется первая часть открытого ключа n: = pq;
- определяется вторая часть открытого ключа — выбирается небольшое нечетное
число е, взаимно простое с числом (р - 1)(q - 1)
(заметим, что (р - 1)(q - 1) = pq(1 - 1/р)(1 - 1/q) =
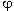 (n));
(n));
- определяется закрытый ключ: d: = е-1 mod ((р - 1)(q - 1)).
После чего открытый ключ (числа n и е) сообщается всем
отправителям сообщений.
- Отправитель шифрует сообщение (разбивая его, если нужно, на слова Si длиной менее log2 n разрядов):
Ci:= (Si)e mod n
и отправляет получателю.
- Получатель расшифровывает сообщение с помощью закрытого ключа d:
Pi:= (Ci)d mod n.
| Теорема |
|---|
|
Шифрование с открытым ключом корректно, то есть в предыдущих обозначениях Pi = Si.
|
Доказательство
Легко видеть, что Рi = (Si)ed mod n. Покажем, что 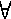 M < n Мed
M < n Мed
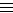 М mod n.
Действительно, числа d и е взаимно обратны по модулю (р - 1)(q - 1), то есть
М mod n.
Действительно, числа d и е взаимно обратны по модулю (р - 1)(q - 1), то есть
ed =1 + k(p-1)(q-1)
при некотором k.
Если М 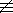 0 (mod р), то по малой теореме Ферма имеем:
0 (mod р), то по малой теореме Ферма имеем:

Если М 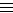 0 (mod р), то сравнение Мed
0 (mod р), то сравнение Мed 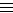 М (mod р), очевидно, выполняется. Таким образом,
М (mod р), очевидно, выполняется. Таким образом,
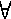 0 <= M < n Med
0 <= M < n Med 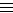 М (mod р).
М (mod р).
Совершенно аналогично имеем
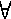 0 <= M < n Med
0 <= M < n Med 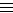 М (mod q),
М (mod q),
и по следствию к китайской теореме об остатках
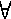 M < n Med
M < n Med 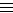 М (mod n).
М (mod n).
Поскольку Si < n и Pi < n, заключаем, что 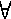 i Рi = Si.
i Рi = Si.
Пример
Генерация ключей:
- р:= 3, q:= 11;
- n:= рq = 3*11 = 33;
- (р - 1)(q - 1) = 2 * 10 = 20, е:= 7;
- d:= 7-1 mod 20 = 3, (7 * 3 mod 20 = 1).
Пусть S1:= 3, S2:= 1, S3:= 2 (S1, S2, S3 < n = 33). Тогда код определяется следующим образом.
- C1:= 37 mod 33 = 2187 mod 33 = 9;
- C2:= 17 mod 33 = 1 mod 33 = 1;
- C3:= 27 mod 33 = 128 mod 33 = 29.
При расшифровке имеем:
- P1:= 93 mod 33 = 729 mod 33 = 3;
- P2:= 13 mod 33 = 1 mod 33 = 1;
- P3:= 293 mod 33 = 24389 mod 33 = 2.
| Замечание |
|---|
|
Шифры с открытым ключом сравнительно просты в реализации, очень практичны (поскольку нет необходимости пересылать по каналам связи закрытый ключ и можно безопасно хранить его в одном месте) и в то же время обладают высочайшей криптостойкостью. Кажется, что дешифровать сообщение несложно: достаточно разложить открыто опубликованное число n на множители, восстановив числа р и q, и далее можно легко вычислить секретный ключ d. Однако дело заключается в следующем. В настоящее время известны эффективные алгоритмы определения простоты чисел, которые позволяют за несколько минут подобрать пару очень больших простых чисел (по 100 и больше цифр в десятичной записи). В то же время неизвестны эффективные алгоритмы разложения очень больших чисел на множители. Разложение на множители числа в 200 и больше цифр потребовало бы сотен лет работы самого лучшего суперкомпьютера. При практическом применении шифров с открытым ключом используют действительно большие простые числа (не менее 100 цифр в десятичной записи, а обычно значительно больше). В результате вскрыть этот шифр оказывается невозможно, если не существует эффективных алгоритмов разложения на множители (что очень вероятно, хотя и не доказано строго).
|
6. Цифровая подпись
Шифр с открытым ключом позволяет выполнять и многие другие полезные операции,
помимо шифрования и посылки сообщений в одну сторону. Прежде всего,
для организации многосторонней секретной связи каждому из участников
достаточно сгенерировать свою пару ключей (открытый и закрытый),
а затем сообщить всем партнерам свой открытый ключ.
Заметим, что операции зашифровки и расшифровки по существу одинаковы,
и различаются только показателем степени, а потому коммутируют:
М = (Me)d mod n = Мed
mod n = Мde mod n = (Мe)d mod n = М.
Это обстоятельство позволяет применять различные приемы, известные
как цифровая (или электронная) подпись.
Рассмотрим следующую схему взаимодействия корреспондентов
Х и Y. Отправитель Х кодирует сообщение S
своим закрытым ключом (С:= Мd mod n) и посылает получателю
Y пару <S, С>, то есть подписанное сообщение.
Получатель Y, получив такое сообщение, кодирует подпись сообщения
открытым ключом X, то есть вычисляет S':= Cе mod n.
Если оказывается, что S = S', то это означает, что (нешифрованное!)
сообщение S действительно было отправлено корреспондентом X.
Если же S 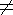 S', то сообщение было искажено при передаче или
фальсифицировано.
S', то сообщение было искажено при передаче или
фальсифицировано.
| Отступление |
|---|
|
В подобного рода схемах возможны различные проблемы, которые носят уже не математический, а социальный характер. Например, допустим, что злоумышленник Z имеет техническую возможность контролировать всю входящую корреспонденцию Y незаметно для последнего. Тогда, перехватив сообщение X, в котором сообщался открытый ключ е, злоумышленник Z может подменить открытый ключ Х своим собственным открытым ключом. После этого злоумышленник сможет фальсифицировать все сообщения Х подписывая их своей цифровой подписью, и, таким образом, действовать от имени X. Другими словами, цифровая подпись удостоверяет, что сообщение S пришло из того же источника, из которого был получен открытый ключ е, но не более того.
|
Можно подписывать и шифрованные сообщения. Для этого отправитель Х сначала кодирует своим закрытым ключом сообщение S, получая цифровую подпись С, а затем кодирует полученную пару <S, С> открытым ключом получателя Y. Получив такое сообщение, Y сначала расшифровывает его своим закрытым ключом, а потом убеждается в подлинности полученного сообщения, сравнив его с результатом применения открытого ключа Х к подписи С.
| Замечание |
|---|
|
К сожалению, даже эти меры не смогут защитить от злоумышленника Z, сумевшего подменить открытый ключ X. Конечно, в этом случае Z не сможет дешифровать исходное сообщение, но он сможет подменить исходное сообщение фальсифицированным.
|
Комментарии
Вопросы, затронутые в этой главе, очень существенны для практических информационных технологий, которые невозможны без кодирования, сжатия данных и шифрования. Разумеется, в реальных современных программах применяются более изощренные, по сравнению с описанными здесь простейшими вариантами, методы. Шифрованию посвящено множество специальных монографий.
Упражнения:
- Является ли схема алфавитного кодирования
<а 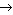 0, b
0, b 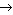 10, c
10, c 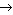 011, d
011, d 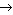 1011, е
1011, е
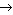 1111>
1111>
префиксной? разделимой?
- Построить оптимальное префиксное алфавитное кодирование для алфавита {а, b, с, d} со следующим распределением вероятностей появления букв:
ра = 1/2, рb = 1/4, рс = 1/8, pd = 1/8.
- Показать, что для несимметричных ошибок функция

является расстоянием.
- Проследить работу алгоритма сжатия Лемпела—Зива на примере следующего исходного текста: abaabaaab.
- Пусть в системе программирования имеется процедура Randomize, которая получает целочисленный параметр и инициализирует датчик псевдослучайных чисел, и функция без параметров Rnd, которая выдает следующее псевдослучайное число в интервале [0, 1]. Составить алгоритмы шифровки и расшифровки с закрытым ключом.
[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
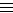 b (mod n)), если а и b при делении на n дают один и
тот же остаток:
b (mod n)), если а и b при делении на n дают один и
тот же остаток: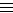 b (mod n): = a mod n = b mod n.
b (mod n): = a mod n = b mod n.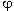 (n): = |Z*n| называется
функцией Эйлера.
(n): = |Z*n| называется
функцией Эйлера.
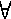 a
a 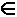 Z*n aφ(n)
Z*n aφ(n) 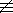 0 (mod р), то по малой теореме Ферма имеем:
0 (mod р), то по малой теореме Ферма имеем:
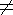 S', то сообщение было искажено при передаче или
фальсифицировано.
S', то сообщение было искажено при передаче или
фальсифицировано.
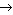 0, b
0, b 