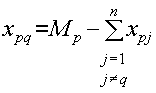
Из линейной алгебры известно, что если ранг системы линейных уравнений равен r и некоторые r переменных системы выражены через остальные переменные, то эти r переменных можно взять за основные (базисные). Из условия данной теоремы следует, что число заполненных клеток равно m + n — 1, т. е. равно рангу системы (7.4), (7.5) (см. пояснения к методу "северо-западного" угла). Поэтому теорема будет доказана, если показать, что переменные, соответствующие заполненным клеткам, могут быть выражены через переменные, соответствующие свободным клеткам.
Предположим, что переменные заполненных клеток, возникшие на первых t шагах метода, где t = 1, 2, ..., m + n — 2, можно выразить через переменные, соответствующие свободным клеткам тех строк и столбцов, которые были вычеркнуты (выпали из рассмотрения) на первых t шагах. Пусть на (t + 1)-м шаге метода заполнена (p, q)-я клетка и из рассмотрения выпала, например, p-я строка. Выразим переменную x_pq из уравнения баланса по p-й. строке:

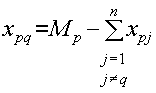
Пусть среди переменных правой части последнего равенства есть переменные клеток, заполненных на одном из первых t шагов. Тогда по предположению их можно выразить через переменные свободных клеток тех строк и столбцов, которые были вычеркнуты на первых t шагах. В случае, если на (t + 1)-м шаге из рассмотрения выпал q-й столбец, x_pq следует выразить из уравнения баланса по q-му столбцу. Подобные рассуждения следует последовательно провести для каждого из шагов заполнения таблицы поставок.
Назад