[Список тем] [Вступление к этой теме] страницы темы: [1] [2] [3]

Нахождение первоначального базисного распределения поставок.

Одним из возможных методов нахождения первоначального базисного распределения поставок является метод "северо-западного "угла, показанный в следующем примере.

Задача 7.2

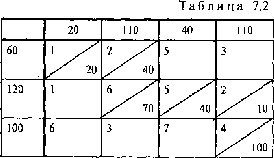
Найти первоначальное базисное распределение поставок для транспортной задачи 7.1. Решение. Дадим переменной х11 максимально возможное значение или, иными словами, максимально возможную поставку в клетку (1,1) - "северо-западный" угол таблицы поставок: х11 = min {60, 20} = 20. После этого спрос 1-го потребителя будет полностью удовлетворен, в результате чего первый столбец таблицы поставок выпадет из последующего рассмотрения (заполненные клетки будем перечеркивать сплошной линией (см. табл. 7.2) клетки, выпавшие из последующего рассмотрения, перечеркнуты пунктирной линией. В таблице поставок найдем новый "северо-западный" угол - клетку (1,2) и дадим в нее максимально возможное значение. Учитывая, что 1-й поставщик уже отдал 20 единиц груза и у него осталось только 40 = 60 - 20 единиц груза, получаем, что х = min {40, 110} = 40. После этого мощность 1-го поставщика полностью реализована и из рассмотрения выпадет первая строка таблицы поставок (перечеркиваем сплошной линией клетку (1,2) и пунктирной линией оставшиеся свободные клетки первой строки). В оставшейся таблице снова находим "северо-западный угол" и т. д. В результате получаем следующее исходное распределение поставок (табл.7.2).

Число заполненных клеток в полученном распределении оказалось равным m + n - 1 = 3+4-1 = 6, т.е. числу основных (базисных) переменных. Это не случайно. Действительно, на каждом шаге (кроме последнего) данного метода из рассмотрения выпадали либо строка, либо столбец, а на последнем шаге и столбец, и строка. Поэтому число заполненных клеток (число шагов) на единицу меньше, чем сумма числа строк и столбцов таблицы поставок, т.е. равно m + n - 1. Оказывается (см. теорему 7.2), что эта особенность шагов метода "северо-западного" угла служит причиной того, что полученное распределение является базисным.
Существенный недостаток метода "северо-западного" угла состоит в том, что он построен без учета значении коэффициентов затрат задачи. С другой стороны, данный метод допускает модификацию, лишенную этого недостатка: на каждом шаге максимально возможную поставку следует давать не в "северо-западную" клетку оставшейся таблицы, а в клетку с наименьшим коэффициентом затрат. При этом распределение поставок оказывается, вообще говоря, ближе к оптимуму, чем распределение, полученное методом "северо-западного угла". Такой метод получения опорного плана называется методом наименьших затрат. Рассмотрим его на следующем примере.

Задача 7.3

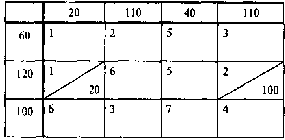
Найти методом наименьших затрат первоначальное распределение поставок в задаче 7.1. Решение. Находим в таблице поставок (см. табл. 7.1) клетки с наименьшим коэффициентом затрат. Таких клеток две - (1,1) и (2,1) с коэффициентами затрат, равными 1. Сравним максимально возможные поставки для этих клеток: для клетки (1,1) х11 = min {60, 20} = 20, для клетки (2,1) х21 = min {120, 20} = 20. Так как они совпадают, то максимально возможную поставку даем в любую из них. Например, даем поставку, равную 20 единицам, в клетку (2,1). В результате спрос первого потребителя удовлетворен и первый столбец таблицы поставок выпадает из последующего рассмотрения . В оставшейся таблице наименьшим коэффициентом затрат обладают две клетки: c12 = c24 = 2. Сравним максимально возможные поставки для этих клеток: для клетки (1,2) х12 = min {60, 110} = 60; для клетки (2,4) х24 = min {120-20, 110} = 100. Даем поставку в клетку (2,4), для которой максимально возможная поставка оказалась больше: х24 = 100. При этом из рассмотрения выпадает вторая строка таблицы поставок (табл. 7.4). 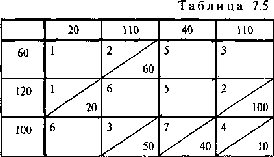Аналогично, продолжая заполнение таблицы поставок шаг за шагом, получаем х12 = min{60, 110} = 60, х32 = min{100, 110-60} = 50, х34 = min {100-50, 110-100} = 10, х33 = min {100-60, 40} = 40 (табл. 7.5)

Сравним найденное распределение поставок с распределением, полученным для той же задачи по методу "северо-западного" угла (см. задачу 7.2, табл. 7.2). Вычислим для каждого из этих распределений суммарные затраты в денежных единицах:
в задаче 7.2:
f₀ = 1 * 20 + 2 * 40 + 6 * 70 + 5 * 40 + 2 * 10 + 4 * 100 = 1140 ;
в задаче 7.3:
f₀ = 1 * 20 + 2 * 60 + 3 * 50 + 2 * 100 + 7 * 40 + 4 * 10 = 810.
Как и ожидалось, при использовании метода "северо-западного" угла суммарные затраты больше, чем при применении метода наименьших затрат. Таким образом, во втором случае мы находимся ближе (по числу необходимых шагов) к оптимуму, чем в первом. Докажем, что распределения, получаемые с помощью указанных методов, являются базисными, и рассмотрим те особые случаи, которые могут встретиться при использовании этих методов.

Теорема 7.2
Пусть на каждом шаге заполнения таблицы поставок возникает одна заполненная клетка, причем из дальнейшего рассмотрения на каждом (кроме последнего) шаге выпадает либо одна строка, либо один столбец. Тогда переменные, соответствующие заполненным клеткам, можно принять за базисные.

(см.доказательство)

Из теоремы 7.2 следует, что методы "северо-западного" угла и наименьших затрат приводят к базисным распределениям поставок, если на каждом (кроме последнего) шаге из рассмотрения выпадают либо одна строка, либо один столбец.

[Список тем] [Вступление к этой теме] страницы темы: [1] [2] [3] [В начало страницы]