[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
[3]
[4]
Понятие подмножества
| Определение |
|
Множество Х является
подмножеством множестваY, если любой элемент
множества Х принадлежит и множествуY
|
Пусть Y—множество студентов группы, а Х—
множество отличников той же группы. Так как
каждый отличник группы является в то же время
студентом этой группы, то множество Х
является подмножеством множества Y.
Многие определения теории множеств удобно
давать в виде математических выражений,
содержащих некоторые логические символы. Для
определения подмножества используем два таких
символа.
 - символ,
называемый квантором общности и означающий
любой, каков бы ни был, "для всех";
- символ,
называемый квантором общности и означающий
любой, каков бы ни был, "для всех";
 - символ следствия (импликации),
означающий "влечет за
собой". Определение подмножества, которое
может быть сформулировано в виде: для любого x
утверждение "x принадлежит X" влечет
за собой утверждение "x принадлежит У",
запишется так:
- символ следствия (импликации),
означающий "влечет за
собой". Определение подмножества, которое
может быть сформулировано в виде: для любого x
утверждение "x принадлежит X" влечет
за собой утверждение "x принадлежит У",
запишется так:
 (1)
(1)
Более краткой записью выражения "X
является подмножеством У"будет запись
 (2)
(2)
что читается как "У содержит X".
Используемый здесь символ  означает включение. Если
желают подчеркнуть, что У содержит и другие
элементы, кроме элементов из X, то используют
символ строгого включения
означает включение. Если
желают подчеркнуть, что У содержит и другие
элементы, кроме элементов из X, то используют
символ строгого включения  :
:
Х  У .
(3)
У .
(3)
Связь между символами  и
и  дается выражением
дается выражением
Х  У
У  X
X
 У и
Х
У и
Х 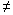 У .
(4)
У .
(4)
Здесь использован знак  , означающий
эквивалентность (в смысле “то
же самое, что”). Отметим некоторые свойства
подмножества, вытекающие из его определения:
, означающий
эквивалентность (в смысле “то
же самое, что”). Отметим некоторые свойства
подмножества, вытекающие из его определения:
X  X
(рефлексивность);
X
(рефлексивность);
[X  Y и Y
Y и Y
 Z]
Z]
 X
X
 Z
(транзитивность).
Z
(транзитивность).
Несколько труднее видеть, что для любого
множества М
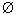
 M. (5)
M. (5)
Действительно, пустое множество 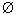 не содержит элементов. Следовательно, добавляя к М пустое
множество, мы фактически ничего не добавляем.
Поэтому всегда можно считать, что любое
множество Мсодержит в себе пустое множество
в качестве подмножества.
не содержит элементов. Следовательно, добавляя к М пустое
множество, мы фактически ничего не добавляем.
Поэтому всегда можно считать, что любое
множество Мсодержит в себе пустое множество
в качестве подмножества.
[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
[3]
[4]
 - символ,
называемый квантором общности и означающий
любой, каков бы ни был, "для всех";
- символ,
называемый квантором общности и означающий
любой, каков бы ни был, "для всех"; - символ следствия (импликации),
означающий "влечет за
собой". Определение подмножества, которое
может быть сформулировано в виде: для любого x
утверждение "x принадлежит X" влечет
за собой утверждение "x принадлежит У",
запишется так:
- символ следствия (импликации),
означающий "влечет за
собой". Определение подмножества, которое
может быть сформулировано в виде: для любого x
утверждение "x принадлежит X" влечет
за собой утверждение "x принадлежит У",
запишется так: (1)
(1) (2)
(2) означает включение. Если
желают подчеркнуть, что У содержит и другие
элементы, кроме элементов из X, то используют
символ строгого включения
означает включение. Если
желают подчеркнуть, что У содержит и другие
элементы, кроме элементов из X, то используют
символ строгого включения  :
: X
X
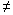 У .
(4)
У .
(4)