 S
имеет место x
S
имеет место x 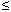 С.
С.
[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3] [4]
Имея дело с множеством вещественных чисел, можно сравнивать элементы этого множества по их значению и, в частности, находить наибольший и наименьший элементы множества. Для конечных множеств, заданных перечислением, эта задача не представляет труда. Так, для множества Т={4, 3, 5, 6} имеем max Т=6, min Т=3. Однако если множество задано описательным способом, например указано лишь правило вычисления числовых значений его элементов, то задача определения наибольшего и наименьшего элементов становится весьма трудной. Несколько более легкой задачей является нахождение лишь области, внутри которой лежат все элементы множества. При решении этой задачи очень полезными являются понятия верхней и нижней границ множества.
Пусть S - множество вещественных чисел.
| Определение |
|---|
Верхней границей S является число С такое,
что для любого x  S
имеет место x S
имеет место x 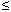 С. С.
|
Чисел, которые могут рассматриваться в качестве
верхней границы множества, может быть бесконечно
много, а может и не быть вообще. Так в множестве m
< S < M любое С  М является верхней границей. Множество
всех целых чисел не имеет верхней границы.
М является верхней границей. Множество
всех целых чисел не имеет верхней границы.
| Определение |
|---|
| Точной верхней границей или супремумом множества S, обозначаемой sup S, называют верхнюю границу, которая не превосходит любую другую верхнюю границу. |
В приведенном выше
примере sup S=M. Множество может иметь только
одну точную верхнюю границу, так как еслиC1
и С2 -две такие границы, то C1 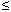 C2 и C2
C2 и C2
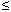 C1 и,
следовательно C1=C2.
C1 и,
следовательно C1=C2.
| Определение |
|---|
Нижней границей множества S является число с
такое, что для любого x
 S имеет место x
S имеет место x  с. с.
|
| Точной нижней границей или инфинумом множества S, обозначаемой inf S, называют нижнюю границу, не меньшую любой другой нижней границы. |
В приводимом примере inf S = m .
| Теорема 2.2. (теорема о верхней и нижней границах подмножества) |
|---|
Если В
 A,
то Inf B A,
то Inf B  inf A; sup inf A; sup
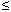 sup A. (2.6) sup A. (2.6) |
 B и b'= inf B.
Но B
B и b'= inf B.
Но B A, т. е.
b'
A, т. е.
b' A. Пусть а'-элемент множества А,
имеющий наименьшее значение, т. е. а'
A. Пусть а'-элемент множества А,
имеющий наименьшее значение, т. е. а' A и
a'=inf A. При этом
если b'=а', тоb'=inf А, если b'
A и
a'=inf A. При этом
если b'=а', тоb'=inf А, если b'
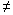 a', то b'
>a'= inf A. Таким образом, b'
a', то b'
>a'= inf A. Таким образом, b'
 inf A или inf B
inf A или inf B
 inf A.
inf A.[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3] [4]