[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
Отношение эквивалентности
Некоторые элементы множества можно рассматривать как эквивалентные
в том случае, когда любой из этих элементов при некотором рассмотрении
может быть заменен другим. В этом
случае говорят, что данные элементы находятся в отношении эквивалентности.
Примерами отношений
эквивалентности являются: отношение “быть на одном курсе” на множестве
студентов факультета;
отношение “иметь одинаковый остаток при делении на З” на множестве
натуральных чисел; отношение
параллельности на множестве прямых плоскости; отношение подобия на
множестве треугольников и т. п.
Для того чтобы дать четкую формулировку
отношения эквивалентности, будем считать, что термин “отношение эквивалентности”
применяется только в случае, если выполняются следующие три условия:
каждый элемент эквивалентен самому себе;
высказывание, что два элемента являются
эквивалентными, не требует уточнения, какой из элементов рассматривается
первым и какой вторым;
два элемента, эквивалентные третьему, эквивалентны между собой.
Примем для обозначения
эквивалентности символ 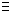 .
Тогда общее
определение эквивалентности получим, записав
три вышеприведенных условия в виде следующих
соотношений:
.
Тогда общее
определение эквивалентности получим, записав
три вышеприведенных условия в виде следующих
соотношений:
х 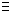 х (рефлексивность);
х (рефлексивность);
х 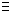 у
у  у
у 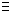 х (симметричность);
х (симметричность);
x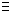 y и y
y и y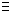 z
z  x
x 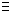 z
(транзитивность).
z
(транзитивность).
Таким образом,
| Определение |
|---|
|
отношение G называется отношением
эквивалентности, если оно рефлексивно, симметрично и транзитивно.
|
Отношение эквивалентности находится в тесной связи с
разбиением множества .
Пусть
Х - множество, на котором определено отношение эквивалентности.
Например, X- множество студентов
курса, а отношением эквивалентности является отношение “быть в одной группе”.
Подмножество
элементов, эквивалентных некоторому элементу х Х, будем называть классом
эквивалентности. Так, группа, в которой учится
студент Иванов, будет классом эквивалентности,
эквивалентным студенту Иванову.
Х, будем называть классом
эквивалентности. Так, группа, в которой учится
студент Иванов, будет классом эквивалентности,
эквивалентным студенту Иванову.
Пусть J - некоторое множество индексов.
Обозначим через {Aj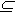 X\j
X\j  J} множество
классов эквивалентности для множества X.
Очевидно, что все элементы одного класса
эквивалентности эквивалентны между собой
(свойство транзитивности) и всякий элемент х
J} множество
классов эквивалентности для множества X.
Очевидно, что все элементы одного класса
эквивалентности эквивалентны между собой
(свойство транзитивности) и всякий элемент х Х может находиться в одном и только в
одном классе. Но таком случае Х является
объединением непересекающихся множеств Аj,
так что полная система классов {AjX\J
Х может находиться в одном и только в
одном классе. Но таком случае Х является
объединением непересекающихся множеств Аj,
так что полная система классов {AjX\J J}
является разбиением множества X. Таким образом,
каждому отношению эквивалентности на множестве
Х соответствует некоторое разбиение множества
на классы Аj.
J}
является разбиением множества X. Таким образом,
каждому отношению эквивалентности на множестве
Х соответствует некоторое разбиение множества
на классы Аj.
Отношение эквивалентности на множестве Х и
разбиение этого множества на классы называют
сопряженными, если для любых х и у из Х отношение
х 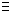 у выполняется тогда и только тогда,
когда х и у принадлежат к одному и тому же классу Aj,
этого разбиения. Более четкому уяснению связи
отношения эквивалентности с разбиением
множества поможет сравнение примеров данного
раздела с примерами из разбиения множества.
у выполняется тогда и только тогда,
когда х и у принадлежат к одному и тому же классу Aj,
этого разбиения. Более четкому уяснению связи
отношения эквивалентности с разбиением
множества поможет сравнение примеров данного
раздела с примерами из разбиения множества.
В качестве общего символа отношения
эквивалентности используют знак 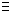 .
Однако для отдельных частных отношений
эквивалентности применяют другие знаки: =
- для обозначения равенства,
|| -параллельности, ↔ -логической эквивалентности.
.
Однако для отдельных частных отношений
эквивалентности применяют другие знаки: =
- для обозначения равенства,
|| -параллельности, ↔ -логической эквивалентности.
[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
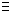 .
Тогда общее
определение эквивалентности получим, записав
три вышеприведенных условия в виде следующих
соотношений:
.
Тогда общее
определение эквивалентности получим, записав
три вышеприведенных условия в виде следующих
соотношений: 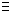 х (рефлексивность);
х (рефлексивность);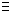 у
у  у
у 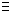 х (симметричность);
х (симметричность);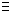 y и y
y и y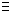 z
z  x
x 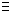 z
(транзитивность).
z
(транзитивность). Х, будем называть классом
эквивалентности. Так, группа, в которой учится
студент Иванов, будет классом эквивалентности,
эквивалентным студенту Иванову.
Х, будем называть классом
эквивалентности. Так, группа, в которой учится
студент Иванов, будет классом эквивалентности,
эквивалентным студенту Иванову. 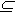 X\j
X\j