[Список тем] [Вступление к этой теме] страницы темы: [1] [2] [3] [4] [5] [6] [7] [8] [9] [10]

Отыскание минимума линейной функции.

При определении минимума линейной функции Z возможны два пути:
1) отыскать максимум функции F, полагая F= -Z и учитывая,
что min(Z) = max(-Z);
2) модифицировать симплексный метод: на каждом шаге уменьшать линейную функцию за счет той неосновной переменной, которая входит в выражение линейной функции с отрицательным коэффициентом.
Рассмотрим это на следующем примере.

Задача 5.2

Решить симплексным методом задачу Z= 18y1 + 16 y2 + 5 y3 + 21 y4 → min при ограничениях: y1 + 2y2 + 3y4 >= 2 3y1 + y2 + y3 >= 3 yi >= 0, i= 1,2,3,4. Решение. Введем дополнительные неотрицательные переменные y5 и y6, со знаком "минус", так как неравенства имеют вид ">= ". Получим систему уравнений: y1 + 2y2 + 3y4 - y5 = 2 3y1 + y2 + y3 - y6 = 3 Если на первом шаге в качестве основных взять дополнительные переменные, то получим недопустимое базисное решение: (0; 0; 0; 0; -2; -3). В данном случае в качестве основных удобно взять переменные y3 и y4 (это согласуется с правилом выбора основных переменных), коэффициенты при y3 и y4 положительны, поэтому в качестве первоначального получим допустимое базисное решение. I ш а г . Основные переменные: y3, y4. Неосновные переменные: y1, у2, у5, у6. Выражаем основные переменные через неосновные: y3 = 3 - 3 y1 - y2+ y6, y4 = (2/3) - (1/3)y1 - (2/3)y2 + (1/3)y5. Y1 = (0; 0; 3; 2/3; 0; 0) - первое базисное решение, оно допустимое. Выражаем линейную функцию через неосновные переменные: Z= 18y1 + 16y2 + 5y3 + 21y4 = 18 y1 + 16y2 + 5(3 - Зy1- y2 + y6) + 21(2/3 - (1/3)y1 - (2/3) y3 + (1/3) y5) = 29 - 4 y1 - Зy2+ 7 y5 + 5y6. Z1 = Z(Y1) = 29 - это значение не является минимальным, так как функцию Z можно уменьшить за счет перевода в основные любой из переменных y1 или y2, имеющих в выражении для Z отрицательные коэффициенты. Так как y1 имеет больший по абсолютному значению коэффициент, то начнем с этой переменной. Для нее наибольшее возможное значение: y1 = min{3/3; (2/3)/(1/3)} = 1, т.е. первое уравнение является разрешающим; y3 становится неосновной переменной, 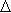Z = -4 * 1 = -4. II шаг. Основные переменные: у1, у4. Неосновные переменные: у2, у3 , y5, у6. Получим после преобразований: y1 =1- (1/3) y2- (1/3) y3 +(1/З) y6, y4 = 1/3 - (5/9) y2 + (1/9) y3 + (1/3) y5 - (1/9)y6 Z =25- (5/3) y2 + (4/3) y3 + 7 y5 + (11/3) y6 - линейная функция. При базисном решении Y1 = (1; 0; 0; 1/3; 0; 0) получаем Z2 = Z(Y2) = 25. Z2 - Z1 = 25 - 29 = -4 = 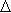Z1. Переменную у2 переводим в основные, так как в выражение для Z она входит с отрицательным коэффициентом. Наибольшее возможное значение y2 = min {3; 3/5} = 3/5, второе уравнение разрешающее, и у4 переходит в неосновные переменные; 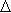Z1 = 3/5(-5/3) = -1. Ill ш а г . Основные переменные: y1, y2. Неосновные переменные: y3, у4, у5, у6. Получим после преобразований: y1 = 4/5 - 2/5 y3 + 3/5 y4 - 1/5 y5 + 2/5 y6, y2 = 3/5 + 1/5 y3 - 9/5 y4 + 3/5 y5 - 1/5 y6,   Z = 24 + y3 + 3 y4 + 6 y5 + 4 y6 . Базисное решение У3 = (4/5; 3/5; 0;0;0;0 ) оптимальное, так как в выражении для Z нет неосновных переменных с отрицательными коэффициентами. Поэтому Zmin = Z3 = Z(Y3) = 24. Z3 - Z2 = 24 -25 = -1 = 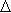Z2

Критерий оптимальности решения при отыскании минимума линейной функции
Если в выражении линейной функции через неосновные переменные отсутствуют отрицательные коэффициенты при неосновных переменных, то решение оптимально.

Замечание.
На каждом шаге симплексного метода какая-либо неосновная переменная переводится в основные, при этом каждое уравнение системы ограничений определяет конечное или бесконечное наибольшее возможное значение этой переменной - оценочное отношение.

В задачах 5.1 и 5.2 встречались различные случаи оценки роста неосновной переменной, которые зависели от знаков и значений свободного члена и коэффициента при переводимой переменной. Сформулируем все возможные случаи. Обозначим: х_i- переводимая неосновная переменная, b_j - свободный член, а_ij - коэффициент при х_i. В общем виде уравнение x_j = b_j + ... + а_ijх_i + ... определяет наибольшее возможное значение х_i по следующим правилам:
1) х_i = | b_j/a_ij |, если b_j и a_ij разного знака и а_ij 0, b_j 0;  например: х₃ = 8 - 2х₂ +:; х₂ = 8/2 =4 или х₃ = -8 + 2х₂ + ...,  х₂ = 8/2 = 4.
2) х_i = , если b_j и a_ij одного знака и а_ij 0, b_j 0; например, х₃ = 8 + 2х₂ +:;  х₂ = .
3) х_i = 0, если b_j = 0 и a_ij < 0, например, x₃ = 0 - 2x₂ + ...;  x₂ = 0.
4) х_i = , если b_j = 0 и a_ij > 0, например, x₃ = 0 + 2x₂ + ...;  x₂= .
5) х_i = , если a_ij = 0, например, x₃ = 5 + 0x₂ + ...; x₃ = -5 + 0x₂ + ...;  x₂ = .

[Список тем] [Вступление к этой теме] страницы темы: [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [В начало страницы]