Задача 5.4
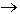max при ограничениях:2x1 + 3x2 >= 12
-x1 + x2 <= 7,
2x1 + x2<= 10,
x2 >= 2,
x1>= 0 x2>= 0
Решение. После введения дополнительных неотрицательных переменных с соответствующими знаками получим систему уравнений:
2x1 + 3x2 - x3 = 12,
-x1 + x2 + x4 = 7,
2x1 + x2 + x5 = 10,
x2 - x6 = 2,
На I шаге выравнивающие переменные возьмем в качестве основных, так как они удовлетворяют правилу: входят во все уравнения и только по одному разу.
I ш а г . Основные переменные: x3, x4, x5, x6. Неосновные переменные: x1, x2.
Выразим основные переменные через неосновные:
x3 = -12 + 2x1 + 3x2,
x4 = 7 + x1 - x2,
x5 = 10 - 2x1 - x2,
x6 = -2 +x2,
X1=(0; 0; -12; 7; 10; -2)
- первое базисное решение недопустимое, с двумя отрицательными компонентами (выделены).
Для получения допустимого базисного решения поступаем так, как в задаче 5.3: выбираем любое уравнение, содержащее отрицательный свободный член (первое или четвертое), например первое, и в нем - любую неосновную переменную с положительным коэффициентом: x1 или x2, например x1. Наибольшее возможное значение x1 = min{12/2;
; 10/2;
} = 5 достигается в третьем уравнении; оно разрешающее, и переменная
x5 переходит в неосновные переменные. Однако при этом ни одна из
отрицательных компонент базисного решения не пропадает! Поэтому невыгодно
переводить переменную x1 в основные переменные. Переведем в
основные x2, тогда наибольшее возможное значение
x2 = min{12/3; 7; 10; 2} = 2 достигается в четвертом
уравнении; при этом переменная x6 переходит в неосновные и исчезает
одна отрицательная компонента в базисном решении.II шаг. Основные переменные: x2, x3, x4, x5. Неосновные переменные: x1, x6.
Выразим новые основные переменные через новые неосновные, начиная с четвертого уравнения:
x2 = 2 +x6,
x3 = -6 + 2x1 + 3x6,
x4 = 5 + x1 - x6,
x5 = 8 - 2x1 - x6.
X2 = (0; 2; -6; 5; 8; 0) - недопустимое базисное решение с одной отрицательной компонентой. Рассмотрим второе уравнение (с отрицательным свободным членом) и переведем в основные одну из неосновных переменных, x1 или x6, входящих в уравнение с положительными коэффициентами.
Получим из уравнений их наибольшие возможные значения:
x1 = min{
; 3; ; 8/2} =
3 достигается во втором уравнении;x6 = min{
; 2; 5; 8} = 2 тоже определяет второе уравнение как
разрешающее. Любой выбор устранит недопустимость решения, поэтому безразлично,
какую переменную x1 или x6 выбрать. Переведем
x6, в основные.III шаг. Основные переменные: x2, x4, x5, x6. Неосновные переменные: x1, x3.
Выразим новые основные переменные через новые неосновные, начиная со второго уравнения:
x6 = 2 - (2/3)x1+ (1/3)x3,
x2 = 4 - (2/3)x1+ (1/3)x3,
x4 = 3 + (5/3)x1 - (1/3)x3,
x5 = 6 - (4/3)x1+ (1/3)x3,
X3 = (0; 4; 0; 3; 4; 2) - допустимое базисное решение. Выражаем функцию цели через неосновные переменные F = -2x1 + 3x2 = 12 - 4x1 + x3.