Задача 5.7.
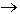max при ограничениях:x1 + x2 <= 8,
2x1 - x2 >= 1,
x1 - 2x2 <= 2,
x1>= 0, x2 >= 0
Решение. Геометрическое решение задачи приведено в задаче, а (см. рис. 4.5, а): оптимум достигается в любой точке отрезка АВ, так как линия уровня параллельна этому отрезку. Покажем, как проявляется наличие альтернативного оптимума при решении задачи симплексным методом. На очередном шаге получаем:
основные переменные: x1, x2, x5, неосновные переменные: x3, x4. Выражаем основные переменные через неосновные:
x1 = 5 - (2/3)x3 - (1/3)x4,
x2 = 3 - (1/3)x3 + (1/3)x4,
x5 = 9 - x3 - x4,
Х1 = (3; 5; 0; 0; 9) - допустимое базисное решение, соответствующее угловой точке А(3; 5). Линейная функция: F = 24 - x3. В этом выражении отсутствуют положительные коэффициенты при неосновных переменных, значит критерий оптимальности выполнен, X1 - оптимальное базисное решение, Fmax = F(X1) = 24. Однако в последнем выражении для F отсутствует неосновная переменная x4 (формально входит с нулевым коэффициентом), поэтому изменение этой переменной не повлечет за собой изменение линейной функции. Например, можно перевести в основную переменную x4; x4 = min{15;
; 9} = 9. Переменная x5 перейдет в неосновные, однако изменения
линейной функции не произойдет: D
F = 9 0 = 0. Действительно, на следующем шаге получим новое базисное
решение X2 = (6; 2; 0; 9; 0), соответствующее угловой точке В (6; 2),
Fmax = F(X2) = 24. Учитывая, что переменная x3 = 0 (в базисном
решении X2 она осталась неосновной), а переменная x4 удовлетворяет
неравенству 0 <= x <= 9, из системы уравнений можно получить все
множество оптимальных решений задачи. Положим для удобства x4 = t,
где t принадлежит интервалу
[0; 9]. Тогда множество оптимальных решений: x1 = 3 + (1/3)t,
x2 = 5 - (1/3)t, x3 = 0; x4 = t; x5
= 9 + t (t принадлежит интервалу [0; 9]).