Задача 5.5.
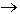 min
minпри ограничениях:
3x1 + x2 >= 9
x1 + 2x2 >= 8
x1 + 6x2 >= 12,
x1 >= 0, x2 >= 0
Решение. Введем выравнивающие переменные x3, x4, x5, (каждую со знаком "минус"). Их экономический смысл - это разность между содержанием и необходимым минимумом каждого из питательных веществ.
На I шаге берем дополнительные переменные в качестве основных.
I шаг . Основные переменные: x3, x4, x5. Неосновные переменные: x1, x2.
После преобразований получим:
x3 = -9 + 3x1 + x2,
x4 = -8 + x1 + 2x2,
x5 = -12 + x1 + 6x2,
Х1 = (0; 0; -9; -8; -12) - первое базисное решение недопустимое, содержащее три отрицательные компоненты. Неосновная переменная x2 входит в каждое уравнение с положительным коэффициентом, поэтому имеет смысл перевести ее в основные. В случае, когда все основные переменные принимают отрицательные значения, для ускорения решения можно в качестве значения для переменной x2 взять максимальное оценочное отношение из полученных во всех уравнениях: x2 = max{9/3; 8; 12} = 12. Третье уравнение является разрешающим, при этом x5 = 0 и переходит в основные, а остальные основные переменные принимают положительные значения.
II шаг. Основные переменные: x2, x4, x5.Неосновные переменные: x1, x3.
После преобразований получим:
x2 = 9 - 3x1 + x3,
x4 = 10 - 5x1 + 2x3,
x5 = 42 - 17x1 + 6x3,
X3 = (0; 9; 0; 10; 42) - допустимое базисное решение. Если действовать, как в предыдущих примерах, то для получения допустимого решения потребуется три шага.
Заканчивая решение задачи 5.5 симплексным методом (рекомендуем это сделать самостоятельно), на следующем шаге получаем оптимальное базисное решение X3 = (2; 3; 0; 0; 5), при котором минимальные затраты на рацион составляют Fmin = 26. Учитывая экономический смысл исходных и дополнительных переменных, получаем, что в оптимальном рационе используются 2 единицы корма I и 3 единицы корма II, при этом вещества S1 и S2 потребляются в необходимых минимальных количествах (x3 = x4 = 0), а питательное вещество S3 оказывается в избытке на 5 единиц (x5 = 5).