Задача 5.6. |
Решить симплексным методом задачу
F = x1 + 3x2  max max
при ограничениях:
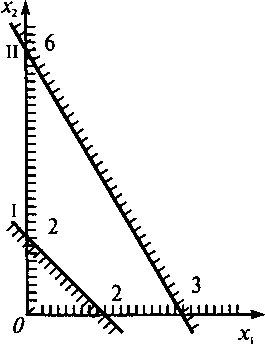
x1 + x2 <= 2,
2x1 + x2 >= 6,
x1>= 0, x2 >= 0
Решение. Введем выравнивающие переменные:
x1 + x2 + x3 = 2,
2x1 + x2 - x4 = 6,
I ш а г . Основные переменные: x3 , x4 ,
Неосновные переменные: x1 ,x2 .
x3 = 2 - x1 - x2,
x4 = -6 + 2x1 + x2,
Х1 = (0; 0; 2; -1) - недопустимое базисное решение. Во втором
уравнении выбираем любую переменную - x1 или x2,
так как обе имеют знак "плюс", и переводим в основные. Для x1:
min{2;6/2) = 2,
разрешающее первое уравнение; для x2: min (2;6) = 2, разрешающее
тоже первое уравнение, поэтому в любом случае не удается сразу избавиться от
отрицательной компоненты базисного решения.
II шаг. Основные переменные: x1, x4.
Неосновные переменные: x2, x3.
Получим после преобразований:
x1 = 2 - x2 - x3,
x4 = -2 - x1 - 2x3,
X2 = (2; 0; 0; -2) - недопустимое базисное решение. Однако
второе уравнение не содержит неосновной переменной с положительным
коэффициентом, поэтому невозможно увеличить переменную x4 и
получить допустимое базисное решение. Ограничения - противоречивы. Задача не
имеет решения (см. рис.)
|
| Алгоритм получения первоначального допустимого базисного решения: |
|---|
1. Если каждая выравнивающая переменная входит в уравнение с тем же знаком,
что и свободный член, стоящий в правой части уравнения, то выравнивающие
переменные можно брать в качестве основных на I шаге. При этом получится
допустимое базисное решение.
2. Если первое базисное решение получилось недопустимым (например, в качестве
основных взяты выравнивающие переменные, но хотя бы одна из них входила в
уравнение со знаком, противоположным знаку свободного члена), то рассматриваем
уравнение, содержащее отрицательный свободный член (любое, если их несколько),
и переводим в основные ту неосновную переменную, которая в это уравнение
входит с положительным коэффициентом (любую, если их несколько). Такие шаги
повторяем до тех пор, пока не достигается допустимое базисное решение.
3. Если базисное решение недопустимое, а в уравнении, содержащем отрицательный
свободный член, отсутствует неосновная переменная с положительным коэффициентом,
то в этом случае допустимое базисное решение получить невозможно, т.е. условия
задачи противоречивы.
|
 max
max