Задача 5.8.
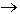max при ограничениях:x1 - x2 <= 2,
3x1 - 2x2 <= 6,
6x1 - 4x2 <= 14,
x1>= 0, x2 >= 0
Решение. После введения выравнивающих переменных, которые возьмем в качестве
основных, получим:
I ш а г . Основные переменные: x3, x4,
x5. Неосновные переменные: x1,
x2.
После преобразований получим:
x3 = 2 - x1 + x2,
x4 = 6 - 3x1 + 2x2,
x5 = 14 - 6x1 + 4x2,
X1= (0; 0; 2; 6; 14) - допустимое базисное решение. F = 2 x1
- x2, F1 = F(X1) = 0.
Критерий оптимальности на максимум не выполнен, поэтому переводим в основные
переменную x1, так как в выражение для F она входит с
положительным коэффициентом: x1 = min{2; 6/3; 14/6}=2.
Оценочные отношения в двух первых уравнениях совпадают, поэтому в качестве
разрешающего можно взять любое из них, например первое.
II шаг. Основные переменные: x1, x4,
x5. Неосновные переменные: x2, x3.
Получим после преобразований:
x1 = 2 + x2 - x3,
x4 = 0 - x2 + 3x3,
x5 = 2 - 2x2 + 6x3,
X3 = (2; 0; 0; 0; 2) - вырожденное базисное решение,
основная компонента x4 = 0.
Линейная функция цели, выраженная через неосновные переменные, имеет вид:
F = 4 + x2 - 2x3. Переводя переменную
x2 в основные, получаем: x2 =
min{
; 0; 1} = 0, поэтому на следующем шаге изменения функции цели не произойдет,
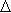F = 0 * 1 = 0. Это нарушение принципа улучшения решения,
который должен выполняться при использовании симплексного метода, в связи с
чем уточним данный принцип: каждый следующий шаг должен улучшить или,
в крайнем случае, не ухудшить значение линейной функции.
III шаг. Основные переменные: x1, x2,
x5. Неосновные переменные: x3,x4.
Получим после преобразований:
x1 = 2 + 2x3 - x4,
x2 = 0 + 3x3 - x4,
x5 = 2 + 2x4,
Xз = (2; 0; 0; 0; 2) - это базисное решение тоже вырождено.
Покомпонентно оно совпадает с X2, однако формально
отличается набором основных переменных. Выражение линейной функции через
неосновные переменные имеет вид: F= 4 + x3 - x4;
F(X3) = 4.