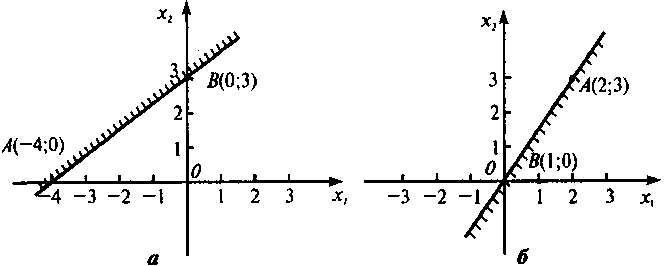
Рис. 2.7
[Список тем] [Вступление к этой теме] страницы темы: [1] [2] [3] [4] [5] [6]
Построить множество решений неравенства:
a) 3x1 - 4x2 + 12 ≤ 0;
б) 3x1 - 2х2 ≥ 0.
Решение. В соответствии с теоремой 2.3, множество решений неравенства есть
полуплоскость.
а) Построим границу полуплоскости - прямую 3x1 - 4x2 +
12 = 0, найдя точки ее пересечения с осями координат А (-4;0) и В
(0;3) на рис. 2.7, a.
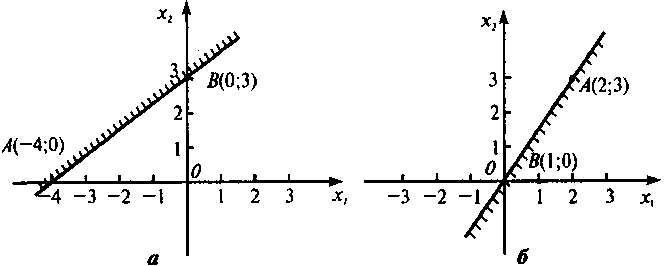
Для определения искомой полуплоскости (верхней или нижней) рекомендуется
задать произвольную контрольную точку, не лежащую на ее границе - построенной
прямой. Если неравенство выполняется в контрольной точке, то оно выполняется и
во всех точках полуплоскости, содержащей контрольную точку, и не выполняется
во всех точках другой полуплоскости. И наоборот, в случае невыполнения
неравенства в контрольной точке, оно не выполняется во всех точках
полуплоскости, содержащей контрольную точку, и выполняется во всех точках
другой полуплоскости.
В качестве контрольной точки удобно взять начало координат О (0;0), не
лежащее на построенной прямой. Координаты точки О не удовлетворяют
неравенству: 3*0 - 4*0 + 12 ≤ 0, следовательно, решением данного неравенства является нижняя
полуплоскость, не содержащая контрольную точку О. Искомая полуплоскость
выделена штриховкой.
б) Построим границу полуплоскости - прямую 3x1 - 4х2
= 0 по двум точкам. Одной из этих точек является начало координат на
рис. 2.7, б (в уравнении прямой отсутствует свободный член), а другую
точку берем на прямой произвольно, например, А (2; 3) на рис. 2.7,
б. В качестве контрольной возьмем, например, точку В (1; 0).
Самую "простую" точку О (0; 0) здесь в качестве контрольной
брать не следует, ибо она лежит на построенной прямой. Так как координаты
контрольной точки В (1; 0) удовлетворяют неравенству, т.е.
3 * 1 - 2 * 0 ≥
0, то решением данного неравенства является нижняя (правая) полуплоскость,
содержащая эту точку.
Учитывая, что множество точек, удовлетворяющих уравнению
a11x1 + a12x2 +
...+a1nxn= b1
при n=3, является плоскостью, а при n>3 - ее обобщением в
n-мерном пространстве - гиперплоскостью, теорему 2.3 можно
распространить на случай трех и более переменных.
| Теорема 2.4 |
|---|
|
Множество всех решений линейного неравенства с n переменными a11x1 + a12x2 +...+ a1nxn≥ b1 является одним из полупространств, на которые все пространство делится плоскостью или гиперплоскостью, включая и эту плоскость (гиперплоскость). |
[Список тем] [Вступление к этой теме] страницы темы: [1] [2] [3] [4] [5] [6] [В начало страницы]