[Список тем] [Вступление к этой теме] страницы темы: [1] [2] [3] [4] [5] [6]

Множество решений систем неравенств.

Рассмотрим множество решений систем неравенств.

Теорема 2.5
Множество решений совместной системы m линейных неравенств с двумя переменными a11x1 + a12x2 ≥ b1 a21x1 + a22x2 ≥ b2 ...       ...        ... am1x1 + am2x2 ≥ bm является выпуклым многоугольником (или выпуклой многоугольной областью).

Каждое из неравенств в соответствии с теоремой 2.3 определяет одну из полуплоскостей, являющуюся выпуклым множеством точек. Множеством решений совместной системы линейных неравенств служат точки, которые принадлежат полуплоскостям решений всех неравенств, т.е. принадлежат их пересечению.
Согласно теореме 2.2 о пересечении выпуклых множеств это множество является выпуклым и содержит конечное число угловых точек, т.е. является выпуклым многоугольником (выпуклой многоугольной областью).

Задача 2.5.

Построить множество решений системы неравенств -5x1 + 4x2 ≤ 20                   (I) 2x1 + 3x2 ≤ 24                   (II) x1 - 3x2 ≤ 3                   (III) x1 ≥ 0                   (IV) 0 ≤ x2 ≤ 6                   (V,VI) Решение. Для построения искомого множества решений системы неравенств строим последовательно множество решений каждого неравенства аналогично тому, как это делалось в задаче 2.4. Рекомендуется после нахождения каждой полуплоскости и выделения ее соответствующей штриховкой находить последовательно их пересечение: сначала полуплоскостей решений первых двух неравенств (многоугольной области GFD на рис. 2.8), затем первых трех неравенств (треугольника GFD), потом - четырех неравенств (четырехугольника HAFD), далее - пяти неравенств (пятиугольника OAFDE) и, наконец, всех шести неравенств - выпуклого многоугольника OABCDE. 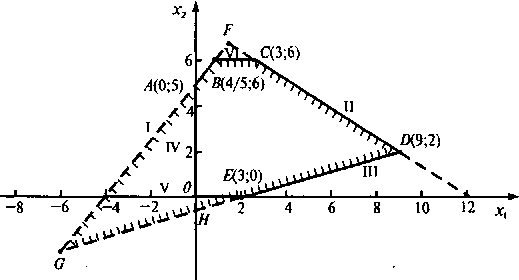Рис. 2.8 Координаты угловых точек - вершин этого многоугольника найдем как координаты точек пересечения соответствующих прямых. Например, точка D является точкой пересечения прямых II и III, т.е. ее координаты являются решением системы 2x1 + 3x2 ≤ 24             (II) x1 - 3x2 ≤ 3             (III) откуда х1 = 9, x2 = 2, т.е. D (9;2). Аналогично находим координаты других угловых точек: О (0;0), А (0;5), В (4/5;6), С (3;6) Е (3;0)

При построении областей решений систем неравенств могут встретиться и другие случаи: множество решений - выпуклая многоугольная область (рис. 2.9, а); одна точка (рис. 2.9, б); пустое множество, когда система неравенств несовместна (рис. 2.9, в).

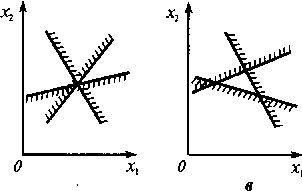
Рис. 2.9

Теорема 2.6
Множество решений совместной системы m линейных неравенств с n переменными является выпуклым многогранником (выпуклой многогранной областью) в n-мерном пространстве.

[Список тем] [Вступление к этой теме] страницы темы: [1] [2] [3] [4] [5] [6] [В начало страницы]