[Список тем] [Вступление к этой теме] страницы темы: [1] [2] [3] [4] [5] [6]

Геометрический метод решения задач. Особые случаи.

Решим геометрически следующие задачи:

Задача a)

F = З x₁ + З x₂ → max при ограничениях
x₁ + x₂ ≤ 8, (I)
2x₁ - x₂ ≥ 1, (II)
x₁ - 2x₂ ≤ 2, (III)
x₁ ≥ 0, x₂ ≥ 0; (IV, V)

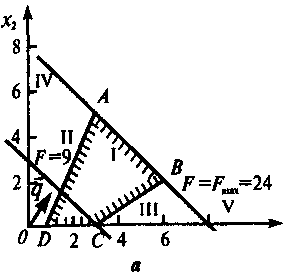
Решение. Геометрическое решение задачи показано на рис. а,.

Из него следует, что линия уровня с максимальным уровнем совпадает с граничной линией АВ многоугольника решений ABCD, т.е. с линией x₁+ x₂= 8. Следовательно, на всем отрезке АВ линейная функция F = З x₁ + З x₂ принимает одно и то же максимальное значение, равное 3(x₁ + x₂) = 3 * 8 = 24. Это означает, что задача имеет бесконечно много оптимальных решений (их задают координаты точек отрезка АВ), среди которых базисных оптимальных решений два - соответственно в угловых точках А(3; 5) и В(6; 2). Точки отрезка АВ задаются уравнением x₂ = 8 - x₁, где 3 ≤ x₁ ≤ 6.
Итак, Fmax = 24 при бесконечном множестве оптимальных решений x₁ = с, x₂ = 8 - с, где 3 ≤ с ≤ 6.

Замечание.

При геометрическом решении подобных задач важно точно установить, действительно ли совпадает линия уровня с границей многоугольника решений или это связано с неточностью построений, мелким масштабом рисунка и т.п. Ответ на этот вопрос будет положительным, если линия уровня и граничная прямая параллельны, т.е. их коэффициенты при переменных пропорциональны. В рассматриваемом примере коэффициенты при переменных линии уровня Р = З x₁ + З x₂ пропорциональны соответствующим коэффициентам граничной прямой x₁ + x₂ = 6.

Задача б)

F = 2 x₁ + З x₂ +1 → min
при ограничениях:
x₁ + x₂ ≥ 4, (I)
2x₁ - x₂ ≥ 1, (II)
x₁ - 2x₂ ≤ 1, (III)
x₁ ≥ 0, x₂ ≥ 0; (IV, V)
Геометрическое решение задачи показано на рис. б,

из которого следует, что если линию уровня перемещать в направлении убывания линейной функции (т.е. в направлении, противоположном вектору q), то она всегда будет пересекать многоугольник решений, следовательно, линейная функция неограниченно убывает.
Итак, конечного оптимума линейной функции нет, т.е. Fmin= -

Если задачу с той же линейной функцией и с той же системой ограничений решать на максимум (F → max), то линию уровня следует перемещать в направлении возрастания F (т.е. в направлении вектора q ), и в этой задаче отсутствует конечный оптимум (см. рис. б): Fmax =
При геометрическом решении задач линейного программирования возможны случаи, когда условия задач противоречивы, т.е. область допустимых решений системы ограничений представляет пустое множество. Очевидно, в таких задачах нет оптимальных решений и нет смысла строить линию уровня.
Рассмотренный геометрический метод решения задач линейного программирования обладает рядом достоинств. Он прост, нагляден, позволяет быстро и легко получить ответ.
Однако только геометрический метод решения никак не может удовлетворить ни математиков, ни экономистов. Возможны погрешности, которые неизбежно возникают при приближенном построении графиков.
Второй недостаток геометрического метода заключается в том, что многие величины, имеющие четкий экономический смысл (такие, как остатки ресурсов производства, избыток питательных веществ и т.п.), не выявляются при геометрическом решении задач. Но самое главное - геометрический метод неприемлем для решения практических задач. Его можно применить только в том случае, когда число переменных в стандартной задаче равно двум. Поэтому необходимы аналитические методы, позволяющие решать задачи линейного программирования с любым числом переменных и выявить экономический смысл входящих в них величин.

[Список тем] [Вступление к этой теме] страницы темы: [1] [2] [3] [4] [5] [6] [В начало страницы]