[Список тем] [Вступление к этой теме] страницы темы: [1] [2] [3] [4] [5] [6]

Геометрический метод решения задач.

Множество допустимых решений (многогранник решений) задачи линейного программирования представляет собой выпуклый многогранник (или выпуклую многогранную область), а оптимальное решение задачи находится, по крайней мере, в одной из угловых точек многогранника решений.
Рассмотрим задачу в стандартной форме с двумя переменными (n = 2).
К такой форме может быть сведена и каноническая задача (с ограничениями в виде уравнений), когда число переменных n больше числа уравнений m на 2, т.е. n - m = 2.

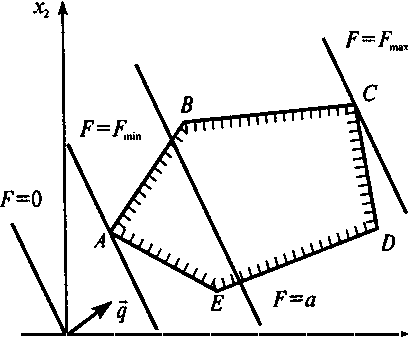
Пусть геометрическим изображением системы ограничении является многоугольник ABCDE. Необходимо среди точек этого многоугольника найти такую точку, в которой линейная функция F = с₁х₁ + с₂ x₂ принимает максимальное (или минимальное) значение.
Рассмотрим так называемую линию уровня линейной функции F, т.е. линию, вдоль которой эта функция принимает одно и то же фиксированное значение а, т.е. F = а, или
с₁х₁ + с₂ x₂ = a.     (4.1)
На многоугольнике решений следует найти точку, через которую проходит линия уровня функции F с наибольшим (если линейная функция максимизируется) или наименьшим (если она минимизируется) уровнем.
Уравнение линии уровня функции (4.1) есть уравнение прямой линии. При различных уровнях а линии уровня параллельны, так как их угловые коэффициенты определяются только соотношением между коэффициентами с₁ и с₂ и, следовательно, равны.
Важное свойство линии уровня линейной функции состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону - только убывает.
Для определения направления возрастания рекомендуется изобразить две линии уровня и определить, на которой из них уровень больше.
Например, одну из линий можно взять проходящей через начало координат (если линейная функция имеет вид F = c₁x₁ + c₂x₂, т.е. без свободного члена, то это соответствует нулевому уровню).
Другую линию можно провести произвольно, так, например, чтобы она проходила через множество решений системы ограничений.
Удобно строить линию уровня для F= НОК (наименьшее общее кратное) c₁ и c₂. Далее, определив направление возрастания линейной функции (обозначим его вектором q), найдем точку, в которой функция принимает максимальное или минимальное значение, подобно тому как на карте находится самая северная или самая южная точка.

Однозначные решения задач.

Решим геометрически задачу:

F = 2x₁ + 3x₂ → max при ограничениях:
x₁ + Зx₂ ≤ 18, (I)
2x₁ + x₂ ≤ 16, (II)
x₂ ≤ 5, (III)
3x₁ ≤ 21, (IV)

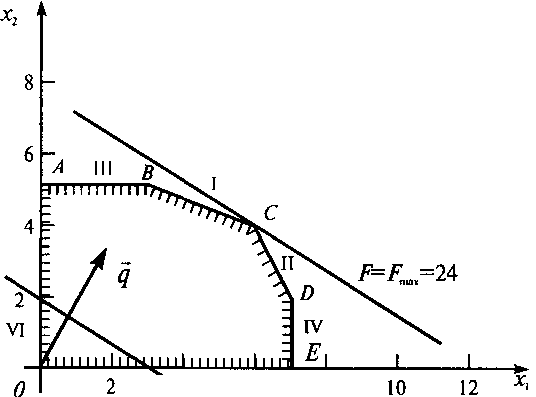
Решение. Изобразим многоугольник решений .
Очевидно, что при F= 0 линия уровня 2x₁+3x₂ = 0 проходит через начало координат (строить ее не обязательно). Зададим, например, F = 6 и построим линию уровня 2x₁ + 3x₂ = 6.
Ее расположение указывает на направление возрастания линейной функции (вектор q ). Так как рассматриваемая задача - на отыскание максимума, то оптимальное решение - в угловой точке С, находящейся на пересечении прямых I и II,
т.е. координаты точки С определяются решением системы уравнений
x₁ + 3x₂ = 18,
2x₁ + x₂ =16
откуда x₁= 6, x₂ = 4, т.е. С(6;4).
Максимум (максимальное значение) линейной функции равен
Fmax=2*6+3*4=24.
т.е. максимальная прибыль в 24руб. может быть достигнута при производстве 6 единиц продукции Р₁ и 4 единиц продукции Р₂.

Решим геометрически задачу о кормовой смеси

F = 4x₁ + 6x₂ ==> min
при ограничениях:
3x₁ + x₂ ≥ 9, (I)
x₁ + 2x₂ ≥ 8, (II)
x₁ + 6x₂ ≥ 12, (III)
x₁ >=0; x₂>=0 (IV ,V)

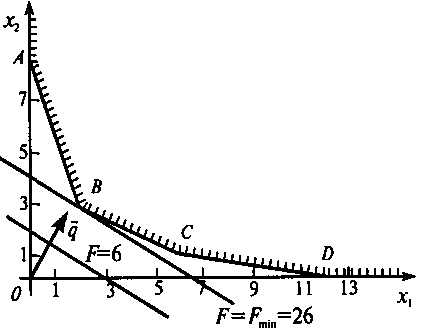
Решение. Многоугольник решений представляет собой неограниченную многоугольную область (не замкнутую).
По расположению линии уровня, например, F = 12 или 4x₁ + 6x₂ = 12, находим направление вектора q (этот вектор указывает на направление возрастания линейной функции).
Очевидно, что точка минимума - это точка В "входа" в многоугольник решений, ибо при дальнейшем перемещении линии уровня в направлении вектора q значения линейной функции увеличиваются.
Находим координаты точки В (2;3), при этом Fmin = 4 * 2 + 6 * 3=26.
Итак, Fmin = 26 при оптимальном решении x₁ = 2, x₂ = 3, т.е. минимальная стоимость рациона 26 руб., если в него включить 2 единицы корма I и 3 единицы корма II.

В рассмотренных задачах максимум и минимум линейной функции достигался в одной точке, так что задачи имели единственное оптимальное решение.
На практике нередко встречаются задачи, которые этим условиям не удовлетворяют. В подобных случаях геометрический метод также позволяет получить ответ.

[Список тем] [Вступление к этой теме] страницы темы: [1] [2] [3] [4] [5] [6] [В начало страницы]