[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
Объединение множеств
| Определение |
| Объединением множеств Х и Y называют
множество, состоящее из всех тех и только тех
элементов, которые принадлежат хотя бы одному из
множеств X, Y, т. е. принадлежат множеству Х
или множеству Y. |
Объединение Х и У
обозначается через X Y.
Формальное определение
Y.
Формальное определение
X  Y={x|x
Y={x|x X или x
X или x
 Y}.
(7)
Y}.
(7)
Объединение множеств иногда называют суммой
множеств и обозначают X+Y. Однако свойства
объединения множеств несколько отличаются от
свойств суммы при обычном арифметическом
понимании, поэтому этим термином мы пользоваться
не будем.
Пример 1. Если Х={1, 2, 3, 4, 5} и У={2, 4, 6, 7},
то X  Y={1, 2, 3,
4, 5, 6, 7}.
Y={1, 2, 3,
4, 5, 6, 7}.
Пример 2. Если X — множество отличников в
группе, Y — множество студентов, проживающих
в общежитии, то X  Y
—множество студентов, которые или
учатся на отлично, или проживают в общежитии.
Y
—множество студентов, которые или
учатся на отлично, или проживают в общежитии.
Пример 3. Рассмотрим два круга, при веденных
на рис. 3. Если Х — множество точек левого
круга, Y — множество точек правого круга, то X
 Y
представляет собой заштрихованную область,
ограниченную обоими кругами.
Y
представляет собой заштрихованную область,
ограниченную обоими кругами.

Рис. 3. Объединение множеств.
Понятие объединения можно распространить и на
большее число множеств. Обозначим через M ={X1,
..., Хn} совокупность n множеств Х1,
..., Хn, называемую иногда системой
множеств. Объединение этих множеств
n
 Xi =
Xi =
 X = X1
X = X1 . . .
. . .  Xn (8)
Xn (8)
i=1
представляет собой множество, состоящее из
всех тех и только тех элементов, которые
принадлежат хотя бы одному из множеств системы M.
Для объединения множеств справедливы
коммутативный и ассоциативный законы
X  Y=Y
Y=Y  X ;
(9)
X ;
(9)
(X  Y)
Y)  Z=X
Z=X
 (Y
(Y Z)=X
Z)=X
 Y
Y
 Z (10)
Z (10)
справедливость которых вытекает из того, что
левая и правая части равенств состоят из одних и
тех же элементов. Далее,
X 
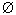 = X. (11)
= X. (11)
Это также очевидное соотношение, так как пустое
множество не содержит элементов, а значит, Х и
Х 
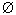 состоят из одних и тех же элементов. Из (11) видно, что пустое множество
состоят из одних и тех же элементов. Из (11) видно, что пустое множество
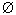 играет роль нуля в
алгебре множеств. Здесь имеет место аналогия с выражением а+0=а
в обычной алгебре.
играет роль нуля в
алгебре множеств. Здесь имеет место аналогия с выражением а+0=а
в обычной алгебре.
[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
 Y.
Формальное определение
Y.
Формальное определение Y={x|x
Y={x|x X или x
X или x
 Y}.
(7)
Y}.
(7) Y={1, 2, 3,
4, 5, 6, 7}.
Y={1, 2, 3,
4, 5, 6, 7}.  Y
—множество студентов, которые или
учатся на отлично, или проживают в общежитии.
Y
—множество студентов, которые или
учатся на отлично, или проживают в общежитии. Y
представляет собой заштрихованную область,
ограниченную обоими кругами.
Y
представляет собой заштрихованную область,
ограниченную обоими кругами.
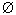 = X. (11)
= X. (11)