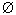[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3] [4] [5] [6] [7] [8]

Формула включений и исключений

Эта формула используется для определения количества элементов в объединении нескольких пересекающихся множеств.

Определение
Мощностью (или модулем) множества называют количество элементов в этом множестве. Обозначается |A|.

Если для двух множеств А и В пересечение не пустое: А&В 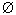, то
|А В| = |А|+ |В| - |А & В|, где
|А| - число элементов множества А,
|В| - число элементов множества B,
|A&B| - число элементов пересечения множеств А и В,
|AB| - число элементов объединения множеств А и В.
Это наглядно видно из рисунка.

Действительно, |А|+ |В| - сумма элементов множеств А и В, причём число общих элементов (красных) в сумму входят дважды.

Рассмотрим случай объединения трёх пересекающихся множеств:
|А B C| = |А| + |B| + |C| -|А&B| - |В & С| - |А & С| + |А&В&С|.

При сложении мощностей трех множеств их общие части (входящие в два множества одновременно) оказываются учтенными дважды, и вычитаются из суммы. Но тогда область пересечения всех трех множеств (красная), окажется трижды прибавленной и трижды удаленной из суммы. Ее элементы надо снова добавить.

Правило объединения для n множеств:
    Для определения количества элементов в объединении нескольких пересекающихся множеств надо
  • сложить количество элементов, входящих в каждое из множеств,
  • вычесть количество элементов, входящих во всевозможные пары множеств,
  • прибавить количество элементов, входящих во всевозможные тройки множеств,
  • ...
  • вычитать количество элементов, входящих одновременно в четное число множеств,
  • прибавлять количество элементов, входящих одновременно в нечетное число множеств.

Этим правилом определяется формула включений и исключений.

Пример 1.
На экзамене по математике было предложено три задачи: одна по алгебре, одна по геометрии и одна по тригонометрии. Из 1000 абитуриентов задачу по алгебре решили 800, по геометрии - 700, по тригонометрии - 600. При этом задачи по алгебре и геометрии решили 600 абитуриентов, по алгебре и тригонометрии 500, по геометрии и тригонометрии 400, а 300 абитуриентов решили все задачи.
Сколько абитуриентов не решили ни одной задачи?

Решение
|I| = 1000 - множество всех абитуриентов,
|А| = 800- множество решивших задачу по алгебре;
|G| = 700- множество решивших задачу по геометрии;
|Т| = 600 множество решивших задачу по тригонометрии;
|A&G| = 600; |A&T| = 500; |G&T| = 400;
|A&G&T| = 300.
|АGТ|- множество всех абитуриентов, решивших хотя бы одну задачу.
По формуле включений и исключений:
|АGТ| = 800+700+600-600-500-400+300=900.
|I|=1000. Тогда множество абитуриентов, не решивших ни одной задачи:
|АGТ| = 1000 - 900 = 100

Пример 2.
Найдите количество натуральных чисел от 1 до 1000, которые не делятся нацело ни на один из простых делителей из следующего множества {2, 3, 5, 7}.

Решение
Обозначим количество чисел данного интервала кратных 2 как |::2|, кратных 2 и 3 как |::2,3| и т.д.
|::2| = |I|\2 = 500 - здесь \ - целочисленное деление с отбрасыванием остатков.
|::3| = |I|\3 = 333
|::5| = |I|\5 = 200
|::7| = |I|\7 = 142
Из 4 делителей можно составить 6 различных пар т. к. С42=6
|::2,3| = |I|\(2*3)= 1000\6 = 166
|::2,5| = |I|\(2*5)= 1000\10 = 100
|::2,7| = |I|\(2*7)= 1000\14 = 71
|::3,5| = |I|\(3*5)= 1000\15 = 66
|::3,7| = |I|\(3*7)= 1000\21 = 47
|::5,7| = |I|\(5*7)= 1000\35 = 28
С43=4
|::2,3,5| = |I|\(2*3*5)= 1000\30 = 33
|::2,3,7| = |I|\(2*3*7)= 1000\42 = 23
|::2,5,7| = |I|\(2*5*7)= 1000\70 = 14
|::3,5,7| = |I|\(3*5*7)= 1000\105 = 9

|::2,3,5,7| = |I|\(2*3*5*7)= 1000\210 = 4
По формуле включений и исключений:
|::2::3::5::7| = 500+333+200+142-166-100-71-66-47-28+33+23+14+9-4=772.
|I|=1000. Тогда множество чисел, не делящихся ни на один из делителей:
|::2::3::5::7| = 228

[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3] [4] [5] [6] [7] [8]