[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3] [4] [5] [6] [7] [8]

Пересечение множеств

Пересечение множеств Х и У обозначается через Х У. Формальное определение
X Y ={x|x X и x Y}.       (12)
Пересечение множеств иногда называют произведением множеств и обозначают XY. Однако свойства пересечения множеств несколько отличаются от свойств произведения в обычном арифметическом понимании, поэтому этим термином мы пользоваться не будем.
Пример 4. Для множеств Х и Y в примере 1 X Y={2, 4}.
Пример 5. Для множеств Х и Y в примере 2 Х У— множество отличников группы, проживающих в общежитии.
Пример 6. Рассмотрим два круга, приведенных на рис. 4,а. Если X—множество точек левого круга, Y — множество точек правого круга, то X Y представляет собой заштрихованную область, являющуюся общей частью обоих кругов.

Рис. 4. Пересечение множеств (а) и непересекающиеся множества (б)

Операция пересечения позволяет установить ряд соотношений между двумя множествами. Множества Х и У называют непересекающимися, если они не имеют общих элементов, т. е. если
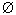X Y= ; .       (13)
Пример 7. Непересекающимися множествами являются:
множества {1, 2, 3} и {4, 5, 6};
множество отличников и множество неуспевающих студентов в группе;
множества точек кругов Х и Y на рис. 4,б.
Говорят, что множества Х и У находятся в общем положении, если выполняются три условия: существует элемент множества X, не принадлежащий У; существует элемент множества У, не принадлежащий X; существует элемент, принадлежащий как X, так и У.
Укажем одно отличие алгебры множеств от алгебры чисел. Если а и b—два числа, то между ними могут быть три соотношения или три возможности:
а<b, а=b, b<а.      (14)
Для множеств Х и У, однако, может не выполняться ни одно из соотношений:
X Y, X=Y, Y X.       (15)
Так, если Х—множество отличников, Y—множество студентов, проживающих в общежитии, то три ранее приведенных соотношения будут означать: Х У —каждый отличник обязательно проживает в общежитии; X=Y—в общежитии проживают все отличники и только они; Y X — все студенты, проживающие в общежитии, являются отличниками.
Очевидно, что эти соотношения не исчерпывают всех возможностей. На самом деле, как вытекает из предыдущих определений, между множествами Х и Y может быть одно из пяти отношений:
X=Y; X Y; Y X; X Y= ; ,
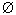X и У находятся в общем положении.
Понятие пересечения можно распространить и на боль шее, чем два, число множеств. Рассмотрим систему множеств M={Х₁, ..., Х_n}. Пересечение этих множеств записывается в виде

      (16)

и представляет собой множество, элементы которого принадлежат каждому из множеств системы M.
Нетрудно видеть, что пересечение множеств обладает коммутативным свойством
X Y=Y X        (17)
и ассоциативным
(X Y) Z = X (Y Z) = X Y Z.       (18) Заметим также, что имеет место соотношение
Х 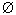= 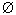,       (19)
аналогичное соотношению а*0=0 в обычной алгебре. Соотношение (19) совместно с соотношением (11) показывает, что пустое множество играет роль нуля в алгебре множеств.

[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3] [4] [5] [6] [7] [8]