[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11]

Отображения

Пусть Х и Y— некоторые множества и G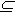 X x Y, причем Пр₁G=X.
Тройка множеств (X, Y, G) определяет некоторое соответствие, обладающее, однако, тем свойством, что его область определения Пр ₁G совпадает с областью отправления, т. е. X , и, следовательно, это соответствие определено всюду на X . Другими словами, для каждого x X существует y Y , так что (х, y) G. Такое всюду определенное соответствие называется отображениемХ в Y и записывается как
G : X Y.(1)
Под словом “отображение” часто понимают однозначное отображение. Однако мы не будем придерживаться этого правила и будем считать, что каждому элементу x X отображение G ставит в соответствие некоторое подмножество
Gх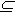 У, (2)

Рис. 11. Геометрическое представление отображения

называемое образом элемента х. Закон, в соответствии с которым осуществляется соответствие, определяется множеством G.
Пример 17. Если в примере 14 исключить из рассмотрения шофера с, то получим отображение G : X Y , в котором Х={а, b}— множество шоферов; Y={ α ,β,} —множество автомашин; G={(a, α ), (а, ), (b, α )}— распределение шоферов по автомашинам. Геометрическое представление этого отображения дано на рис. 11.
Обратимся теперь к рассмотрению некоторых свойств отображения. Пусть A Х. Для любого хА образом х будет множество Gx =Y. Совокупность всех элементов Y, являющихся образами Gx  для всех х А, назовем образом множества А и будем обозначать GА. Согласно этому определению
GА = Gx. (3)
^{х А}
Если А₁ и A₂ — подмножества X, то
G(A₁ A₂)= GA₁GA₂. (4)
Однако соотношение
G(A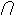_1I A₂) =GA₁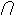GA₂ (5)
справедливо только в том случае, если отображение G : X Y является однозначным. В общем же случае
_{G(A1 A2) GА1GA2}. (6)
Полученные соотношения легко обобщаются и на большее число подмножеств А_i . Так, если А₁, ..., А_n —подмножества X , то

(7) (8)

Поскольку отображение является частным случаем соответствия, для отображения имеют место введенные при рассмотрении соответствий понятия обратного отображения и композиции отображений.

Cвойства отображений

сюръективность

Определение
Отображение f:A → B называется cюръективным, если y (Y)    f-1(y) ≠ Ø
т.е. нет такого образа для которого нет прообраза

инъективность

Определение
Отображение f: A → B называется инъективным, если x1 (X)  иx2 (X)   x1 ≠ x2 → f(x1) ≠ f(x2)
т.е. образы различных прообразов - различны