[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
Отношение порядка
Часто приходится сталкиваться с отношениями,
которые определяют некоторый порядок
расположения элементов множества. Так, мы
отличаем понятия “раньше” и “позже” в случаях,
когда элементами множества являются состояния
динамической системы. Мы отличаем понятия
“больше” и “меньше” и пользуемся при этом
символами > или < , если элементы
множества являются числами. Мы отличаем понятия
множества и подмножества, пользуясь символами 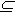 или
или .
.
Во всех этих случаях можно расположить элементы
множества Х или группы элементов в некотором
порядке или, другими словами, ввести отношение
порядка на множестве X.
Различают отношение нестрогого порядка, для
которого используется символ  , и отношение
строгого порядка, для которого используется
символ < . Опишем эти отношения путем
перечисления свойств, которыми они обладают.
, и отношение
строгого порядка, для которого используется
символ < . Опишем эти отношения путем
перечисления свойств, которыми они обладают.
Отношением нестрогого
порядка называют отношение, обладающее
следующими тремя свойствами:
x  x истинно (рефлексивность); x истинно (рефлексивность);
х  y и у y и у  х х  х=у
(антисимметричность); х=у
(антисимметричность);
x  y и у y и у  z z
 х х  z (транзитивность).
z (транзитивность). |
Отношением строгого порядка
называют отношение, обладающее следующими тремя
свойствами:
x < х ложно (антирефлексивность);
x < у и у < х взаимоисключаются
(несимметричность);
x < y и у < z
 х < z (транзитивность). х < z (транзитивность).
|
| Множество Х называют
упорядоченным, если любые два элемента (х и у)
этого множества являются сравнимыми, т. е. х<у
или х=у или у<х. |
[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
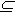 или
или .
.  , и отношение
строгого порядка, для которого используется
символ < . Опишем эти отношения путем
перечисления свойств, которыми они обладают.
, и отношение
строгого порядка, для которого используется
символ < . Опишем эти отношения путем
перечисления свойств, которыми они обладают.
 х=у
(антисимметричность);
х=у
(антисимметричность);