[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11]

Свойства отношений

Как уже указывалось, термин “отношение” используют для обозначения некоторых видов отображений, заданных на одном и том же множестве. В связи с этим удобно вести специальную символику.
Пусть отображение (X, G) является отношением. Рассмотрим элемент у Gх. Будем говорить, что элемент у находится в отношении G к элементу х, и запишем это в виде
уGх. (31)
Так символ G в примере 18 означает отношение “быть детьми данного человека”.
Примечание. Используя для отображения, заданного на одном множестве, соотношение (9), получаем, что отношение есть пара множеств (X, G), в которой G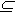Х². Поскольку элементами множества X² являются упорядоченные пары, то можно сказать, что отношение есть множество упорядоченных пар. Так как каждая пара связывает между собой только два элемента множества X², то такое отношение называют бинарным.
Можно ввести более общее понятие отношения, называя отношением пару множества (X, G), где G 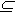Xⁿ. Элементами множества Xⁿ являются упорядоченные n-ки, что позволяет назвать данное отношение n-арным. В частности, множество упорядоченных троек может быть названо тернарным отношением. В дальнейшем, не оговаривая этого особо, под термином “отношение” будем иметь в виду бинарное отношение.

Отношения делятся на различные виды в зависимости от того, обладают или не обладают они некоторыми свойствами.

Рассмотрим шесть основных свойств отношений. При описании этих свойств будем считать, что х, у и z - любые элементы из множества X.

• Рефлексивность: хGх - истинно;
  антирефлексивность: хGх - ложно;
• симметричность: хGу уGх;
  антисимметричность: (хGу и уGх) х = у;
  несимметричность: если хGу - истинно, то уGх - ложно;
• транзитивность: (хGу и yGz) xGz.

Воспользовавшись описанными свойствами, рассмотрим некоторые важные виды отношений.

[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11]