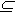[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11]

Функция времени

В основе понятия функции времени лежит множество TR с элементами t, называемое множеством моментов времени. Время обладает той характерной особенностью, что имеет направление. Это означает, что если t₁,t₂ T и t₁<t₂, то момент t₁ предшествует моменту t₂. Другими словами, Т - упорядоченное множество.
Функция времени определяет отображение множества моментов времени Т на множество вещественных чисел R:
F : T R. (22)
Элементами f будут пары (t, х), обозначаемые также через x(t), где t T, x R. Каждая такая пара определяет значение функции в момент t и называется событием или мгновенным значением функции. Полная совокупность пар (t, х), т. е. значений x(t) для всех tT, и представляет собой функцию времени. Дальнейшее уточнение функции времени связано с уточнением ее области определения, т. с. вида множества Т.
Если T=R, т. е. t может принимать любое вещественное значение от   - ∞ до + ∞ то функцию x(t) называют функцией с непрерывным временем, например синусоидальная функция времени x(t) = А sin(w + t + φ), описывающая напряжение в сети переменного тока.
Однако нас обычно не интересуют весьма удаленные моменты времени как в прошлом, так и в будущем. Поэтому производят сужение x(t) на ограниченный интервал t₁< t t₂ , который обычно считают полузакрытым и обозначают (t₁, t₂]. Полузакрытые интервалы времени удобны тем, что допускают последовательное сочленение друг с другом. Так, если интервал(t₁,t₂] разбить моментом t' на два интервал: (t₁, t'] и ( t', t₂], то не будет сомнений, к какому интервалу отнести t'.
Сужение функции x(t), заданной на интервале - ∞ < t < + ∞ , на интервал (t₁, t₂] называют отрезком функции x(t) и обозначают x_(t1,t2]. Итак, по определению
X_(t1,t2] = { x( t )| t ( t₁,t_2] } (23)
Для осуществления операции сужения часто используют специальную функцию времени, называемую единичной функцией или единичным скачком:

(24)

приведенную на рис. 15,а. Так, напряжение, подаваемое на вход прибора, подключаемого к сети в момент t = λ , будет
u(t) = 1(t - )x(t)=1(t - )A sin(w t + φ ).
Другой широко используемой функцией времени является импульсная функция ς (t - ), определяемая соотношениями:

  (25)

которая обращается в импульсную функцию ς (t) при ς 0 . Импульсная функция позволяет выделять мгновенные значения функции x(t)для фиксированных моментов времени. Так, еслиt₁< <t₂,то

(26)

Если множество представляет собой множество натуральных чисел
0, 1, 2, ..., n..,
то говорят о функции с дискретным временем. В этом случае элементы множества Т обозначают через n, так что пара (n, х), обозначаемая также х[n] или x_n, определяет значение функции в момент n. На рис. 2.16 приведен пример функции с дискретным временем.

[Список тем] [Вступление к этой теме] Страницы темы: [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11]