X будет представлять собой
отображение множества Х самого в себя и будет
определяться парой(X, G), (9)
где G
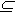Х2 . Подробным изучением
таких отображений занимается теория графов.
Коснемся лишь некоторых операций над подобными
отображениями. Пусть G и d -отображения множества Х в X. Композицией этих отображений назовем отображение Gd , которое в соответствии с правилом, приведенным в § 2.4, определяется так
(Gd )x = G(d x). (10)
В частном случае, если d =G, получаем отображения
G2x = G(Gx) ; (11)
G3x = G(G2x) и т. д. (12)
Таким образом, в общем случае для любого s? 2
Gsx = G(Gs-1x). (13)
Специальным определением введем соотношение
G0x = x. (14)
Это дает возможность распространить соотношение (15) и на отрицательные s. Действительно, согласно (14)
G0x = G(G-1x) = GG-1x = x . (15)
Это означает, что G-1x представляет собой обратное отображение. Тогда
G-2x = G-1(G-1x) (16)
и т. д.
Пример 18. Пусть Х-множество людей. Для каждого человека х
Х обозначим через Gx ;
множество его детей. Тогда G2x -
множество внуков х; G зx - множество
правнуков х ; G-1x - множество
родителей x и т. д. Изображая людей точками и рисуя стрелки, идущие из х в Gх, получаем родословное или генеалогическое дерево (рис. 12).
Пример 19. Рассмотрим шахматную игру. Обозначим через х не которое положение (расположение фигур на доске), которое может создаться в процессе игры, через Х множество всевозможных положении. Тогда Gх для любого x
X будет означать множество положений,
которые можно получить из х, делая один ход
при соблюдении правил игры. При этом Gх= 
,
если х - матовое или патовое положение; G3x
- множество положении, которые можно получить из х
тремя ходами; G-1x -множество положений,
из которых данное положение может быть получено
за один ход.Для отображений, заданных на одном множестве, часто используют некоторые другие названия, которые у нас встретятся в дальнейшем.
