[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
Функция
Рассмотрим некоторое отображение
G : X  Y.
(17)
Y.
(17)
Это отображение называют функцией, если
оно однозначно, т. е. если для любых пар (x1y1)
 f из x2=x1 следует y2=y1.
f из x2=x1 следует y2=y1.
На рис. 1З, а приведен пример отображения,
являющегося функцией. Отображение на рис. 13,б
функцией не является.
Из определения отображения и из приведенных
ранее примеров следует, что элементами множеств Х
и У могут быть объекты любой природы. Однако в
задачах кибернетики большой интерес
представляют отображения, которые являются
однозначными и множество значений которых
представляет собой множество вещественных чисел
R. Однозначное отображение f ,
определяемое (17), называют функцией с
вещественными значениями, если Y 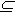 R.
Понятие функции является чрезвычайно широким, и
изучению отдельных классов функций посвящены
многие математические дисциплины (алгебра,
тригонометрия
R.
Понятие функции является чрезвычайно широким, и
изучению отдельных классов функций посвящены
многие математические дисциплины (алгебра,
тригонометрия
Рис. 13. Иллюстрация к понятию функции
и т. п.). Мы рассмотрим только некоторые общие
наиболее фундаментальные свойства функции, не
касаясь свойств конкретных классов.
Пример 20. Из одного города в другой можно
проехать по железной дороге (ж.д.) , автобусом (авт.)
или самолетом (сам.). Стоимость билета будет
соответственно 7, 9 и 12 руб. Стоимость
билета можно представить как функцию от вида
транспорта. Для этого рассмотрим множества Х={
ж.д., авт., сам.}. Y ={7, 9, 12}.
Функция f : X  Y, получаемая из условий примера,
может быть записана в виде множества f={( ж.д.,
7), (авт., 9), (сам., 12)}.
Y, получаемая из условий примера,
может быть записана в виде множества f={( ж.д.,
7), (авт., 9), (сам., 12)}.
Значение у в любой из пар (х, y)  f называют
функцией от данного х и записывают в виде y=f(x).
Такая запись позволяет вести следующее
формальное определение функции:
f называют
функцией от данного х и записывают в виде y=f(x).
Такая запись позволяет вести следующее
формальное определение функции:
f = {(x, y)  X x Y | y = f(x)}. (18)
X x Y | y = f(x)}. (18)
Таким образом, символ f используют при
определении функции в двух смыслах:
f является множеством, элементами которого
будут пары (х, у), участвующие в соответствии;
f(х) является обозначением для y  У,
соответствующего данному х
У,
соответствующего данному х  Х.
Х.
Формальное определение функции в виде
соотношения (18) позволяет установить способы
задания функции.
1. Перечисление всех пар (х, у),
составляющих множество f , как это было
сделано в примере 20. Такой способ задания
функции применим, если Х является конечным
множеством. Для большей наглядности пары (х, у)
удобно располагать в виде таблицы.
2. Во многих случаях как X, так и Y
представляют собой множества вещественных или
комплексных чисел. В таких случаях очень часто
под f(x) понимается формула, т. е. выражение,
содержащее перечень математических операций
(сложение, вычитание, деление, логарифмирование и
т. п.), которые нужно произвести над х  Х,
чтобы получить у.
Х,
чтобы получить у.
Пример 21. Пусть X = Y = R и f = {(x, y)  = R2|y
= x2} . Тогда f(x) = x2
= R2|y
= x2} . Тогда f(x) = x2
Иногда для разных подмножеств множества Х
функции приходится пользоваться различными
формулами. Пусть А1, ..., An -
попарно непересекающиеся подмножества X .
Обозначим через fi(x), i = l, ¬ n
формулу, определяющую у при х  Аi.
Тогда функция
Аi.
Тогда функция
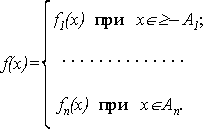
(19)
Так, функцию y = f(x) = |x| можно задать в виде
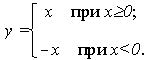
3. Если Х и Y - множества вещественных
чисел, то элементы (х, y) f можно изобразить в
виде точек на плоскости R2. Полная
совокупность таких точек будет представить
собой график функции f(x).
f можно изобразить в
виде точек на плоскости R2. Полная
совокупность таких точек будет представить
собой график функции f(x).
Если в выражении (69) X=U x V, то приходим к
функции от двух переменных u и v ,
обозначаемой через f(u, v), где u  U и
v
U и
v V. Формальное определение функции двух
вещественных переменных будет следующим:
V. Формальное определение функции двух
вещественных переменных будет следующим:
f={(u, v, y)} U x V x Y | y = f(u, v)}. (20)
U x V x Y | y = f(u, v)}. (20)
Аналогично определяют функции от трех и
большего числа переменных.
Свяжем с функцией еще одно понятие, называемое сужением
функции. Пусть f :X  Y - произвольная функция и A
- произвольное множество. Сужением функции f на
множество A называют функцию fA ,
содержащую все те и только те пары (х, y)
Y - произвольная функция и A
- произвольное множество. Сужением функции f на
множество A называют функцию fA ,
содержащую все те и только те пары (х, y)  f,
в которых х
f,
в которых х  А, а значит, (х, y)
А, а значит, (х, y)  A x Y .
Следовательно,
A x Y .
Следовательно,
f A =f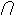 (A x Y). (21)
(A x Y). (21)
Операцию сужения функции часто используют для
табличного задания функций с бесконечной
областью определения X . В качестве множества A
берут обычно выборку равно относящих значений х
множества X. Получаемое при этом сужение fA
функции f уже легко представить в виде
таблицы. По этому принципу построены таблицы
логарифмов, тригонометрических функций и
некоторые другие.
[Список тем]
[Вступление к этой теме]
Страницы темы:
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
 Y.
(17)
Y.
(17) f из x2=x1 следует y2=y1.
f из x2=x1 следует y2=y1.
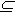 R.
Понятие функции является чрезвычайно широким, и
изучению отдельных классов функций посвящены
многие математические дисциплины (алгебра,
тригонометрия
R.
Понятие функции является чрезвычайно широким, и
изучению отдельных классов функций посвящены
многие математические дисциплины (алгебра,
тригонометрия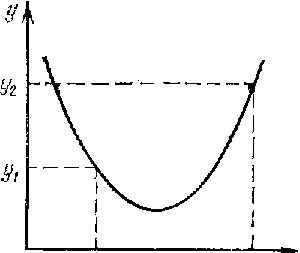
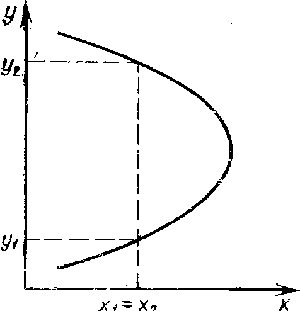
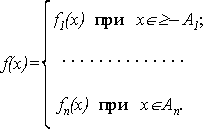
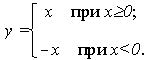
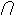 (A x Y). (21)
(A x Y). (21)